원 논문 : Hochreiter, S., & Schmidhuber, J. (1997). Long short-term memory. Neural computation, 9(8), 1735–1780.
“밑바닥부터 시작하는 딥러닝 2”를 옮겼습니다. 그림은 직접 그렸습니다.
RNN의 문제점은 무엇일까?
언어 모델은 현재까지 앞 단어들이 주어지면 다음 단어를 예측한다. 그런데 아래와 같이 긴 문장이 주어진 경우를 보자.
Tom was watching TV in his room. Mary came into the room. Mary said hi to [?]
[?]에 들어갈 단어는 당연히 Tom이다. 모델이 해야할 일은 무엇일까? 앞의 모든 단어가 주어지면 Tom을 가장 높은 확률로 예측하도록 학습해야 한다. 학습 시에 모델에게 정답인 ‘Tom’이 주어졌다고 해보자. 그럼 loss를 역전파하여 파라미터를 업데이트 해야 할텐데, RNN은 이 과정에서 순탄치 못하다. RNN은 맨 앞에 있는 Tom까지 의미 있는 기울기를 전달하기 힘들어하기 때문이다.
왜 그럴까? 결론적으로는 tanh함수와 행렬곱 연산때문에 그렇다. 위의 예에서는 단어가 약 20개 가까이 되는데, 그만큼 tanh 계산도 20번 존재한다. tanh의 미분값은 0~1사이로, 역전파로 한 번 지날 때마다 무조건 기울기가 작아진다. 행렬곱 계산도 마찬가지다. 위의 예로 치면 약 20번 동안 같은 행렬을 계속 곱하는 작업을 하게 된다. 이 행렬곱 노드에서 20번 역전파 하게 되면 기울기 폭발 또는 소실이 쉽게 일어난다.
기울기 폭발의 전통적 해결법은 기울기 클리핑(gradient clipping)이다. 기울기의 L2 norm이 특정 threshold를 넘으면 다시 줄여주는 단순한 방법이다.
그렇다면 기울기 소실은?
이를 해결하려면 RNN의 근본부터 뜯어 고쳐야 하며, 게이트를 추가한 모델인 LSTM과 GRU가 대표적이다. 게이트란 말 그대로 ‘문’이라는 뜻으로, 핵심은 기억 셀이라는 것이 여러 개의 게이트를 통과하며 어떤 정보를 기억할 지, 망각할 지를 학습하게 된다.
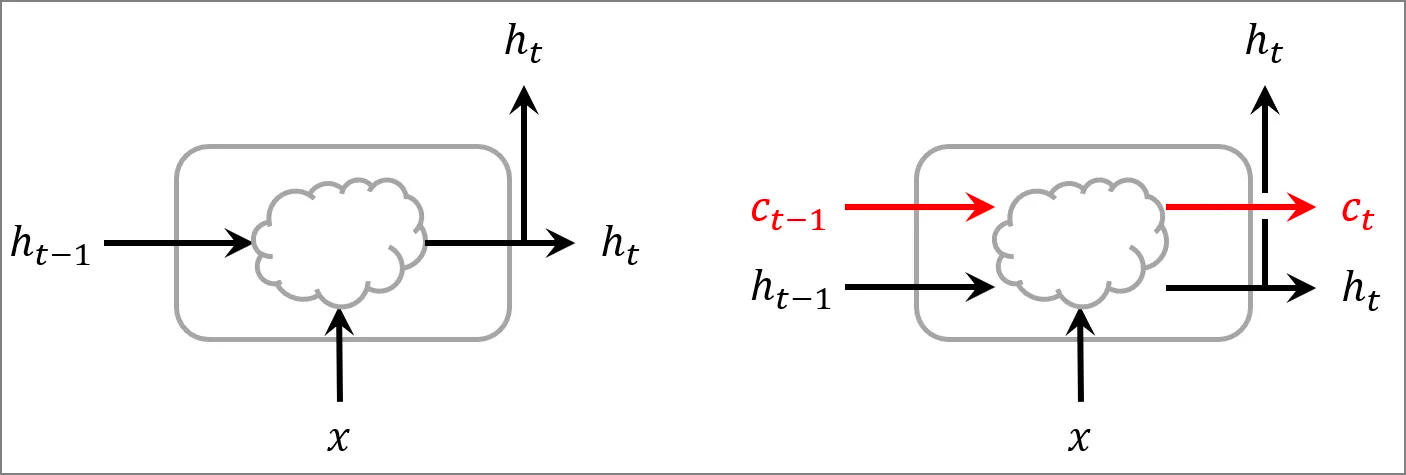
LSTM의 핵심은 기억 셀(memory cell, cell state, c)이다.
이 기억 셀은 외부로는 출력 되지 않는다. 단지 망각해야할 정보, 기억해야 할 정보와 계속 연산해 나간다.
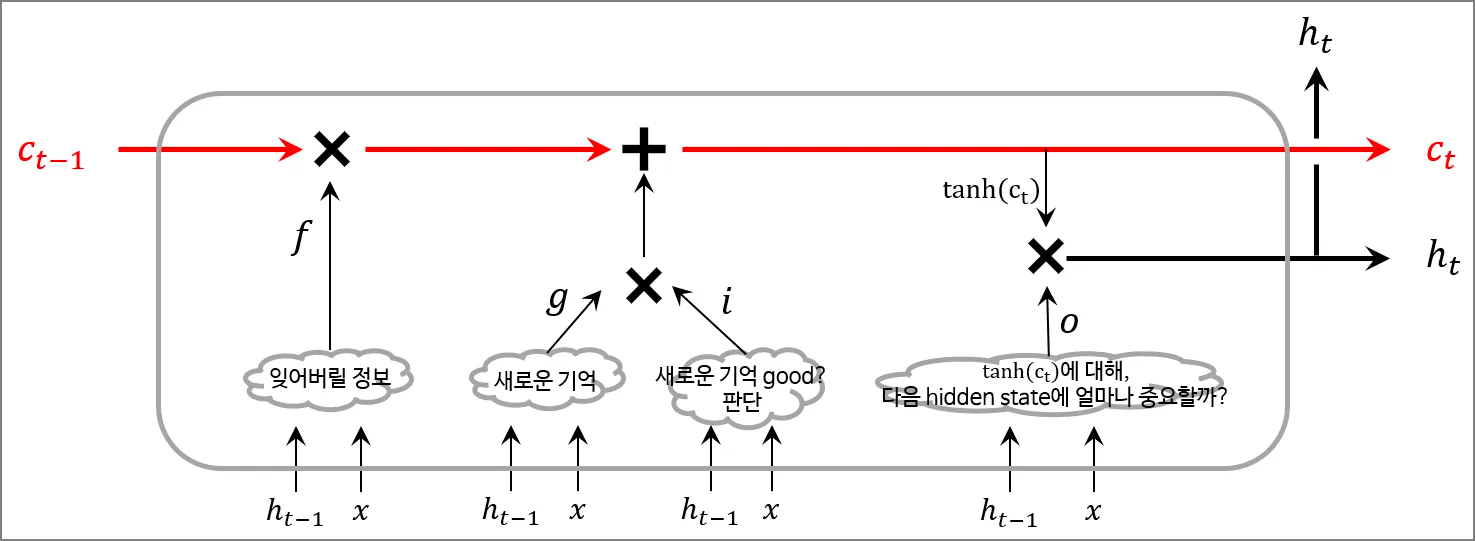
기억 셀 기준으로 어떤 연산이 이루어지는지 살펴보면 편하다. \(c_{t-1}\)이 \(c_t\)로 되는 과정은 위 그림과 같다. 일단 모든 연산이 이전 hidden state인 \(h_{t-1}\)과 현재 인풋 단어 \(x\)로부터 시작한다. 그럼 이제 저 구름 안에서는 어떤 연산이 벌어지는 지를 하나하나 보면 된다.
1. 망각의 문, forget gate
\(c_{t-1}\)가 통과하는 첫 번째 게이트는 망각의 문이다. \(f\)라는 게이트는 아래와 같은 수식으로 얻어진다.
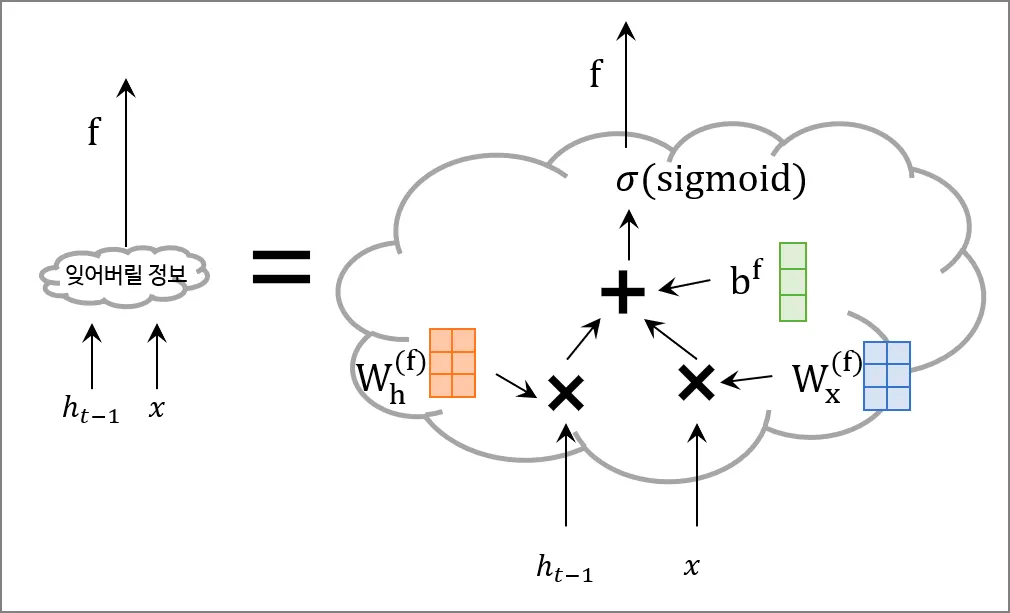
이것이 forget gate이다. 이를 \(c_{t-1}\)과 원소별 곱을 한다.
2. 기억의 문, input gate
다음으로 지날 문은 기억의 문 \(i\)이다. 마찬가지로 \(h_{t-1}\)과 \(x\)를 사용한다. 우선 \(i\)를 구하기 위해선 우선 \(g\)라는 정보가 필요하다. 아래 그림과 같은 연산을 거친 뒤 \(g\)라는 정보가 탄생한다.
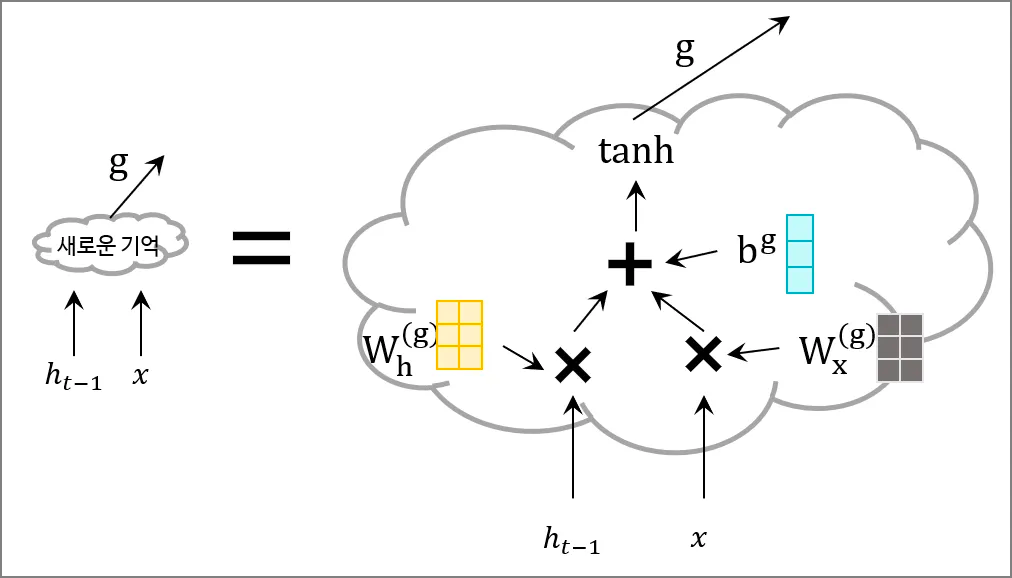
이를 책에서는 ‘새로운 기억 셀’이라고 한다. 원 논문에는 어떤 표현으로 쓰였는지는 잘 모르겠다.
3. 나가는 문, output gate
\(c_t\)에는 과거부터 현재(\(t\))까지, 필요한 모든 정보가 담겨있다. 당장은 그렇지 않더라도 학습을 통해 그렇게 만들어져 갈 것이다. 이 \(c_t\)를 가지고 외부에 출력할 hidden state \(h_t\)를 만들 것이다. \(c_t\)에 \(\tanh\)를 적용하여 \(h_t\)를 만든다.
\[h_t = \tanh(c_t)\]\(c_t\)의 각 원소에 \(\tanh\)를 적용하였다. 근데 마지막으로 한번 더 \(h_t\)에 게이트를 하나 더 지나게 한다. 이를 output gate라고 한다. 이제 이 셀을 나가는 문이다. 문의 이름은 \(o\)이다.
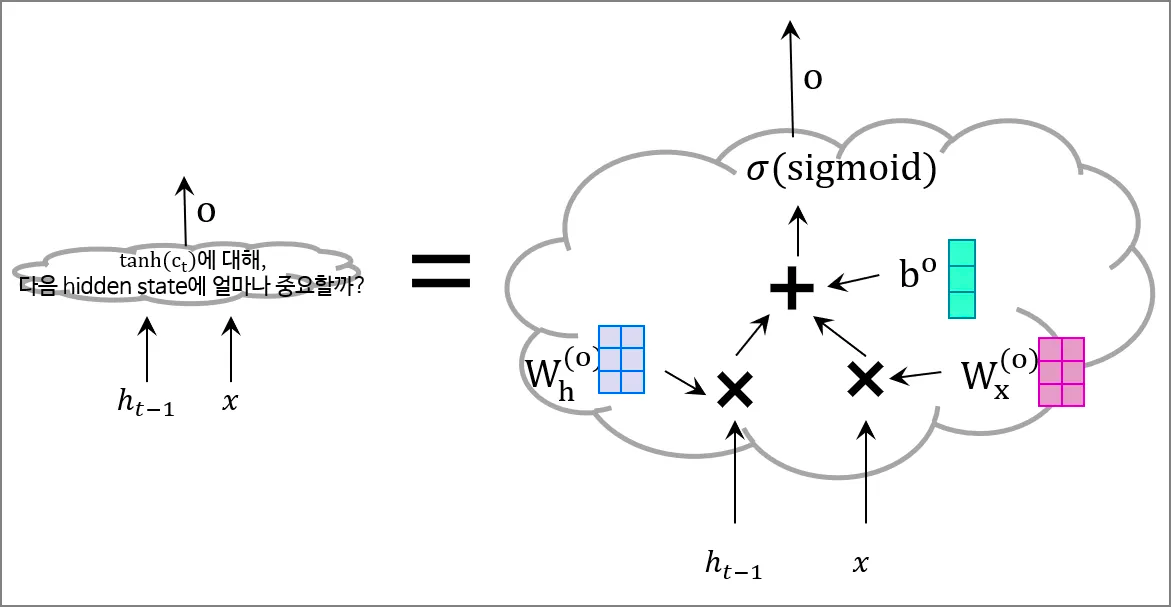
output gate인 \(o\)는 “\(\tanh(c_t)\)가 다음 hidden state \(h_t\)에 얼마나 중요한가”, “\(\tanh(c_t)\)를 얼마나 흘려보낼까?”를 결정한다. 그러므로 \(o\)와 \(\tanh(h_t)\)를 원소별 곱을 수행하면 \(h_t\)를 얻는다.
근데 어떤 건 sigmoid를 쓰고 어떤 것은 tanh를 썼다. tanh의 출력은 -1~+1이다. 이는 ‘인코딩 된 정보의 강약’을 의미할 수 있다. 반면 sigmoid는 0~1의 값이므로 ‘얼마나 흘려보낼 지를 정하는 게이트(문)’이라고 생각할 수 있다. 따라서 게이트에는 sigmoid가, 정보를 품는 작업에는 tanh가 쓰인다.
이 문들이 어떤 원리로 “기울기 소실 문제”를 해결한단 말일까?
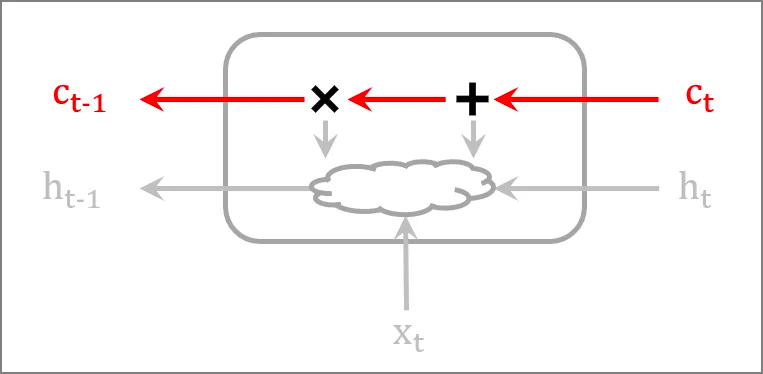기억 셀의 역전파
기억 셀의 역전파를 보면, 더하기와 곱하기 밖에 없다. 더하기는 역전파 시 그대로 흘러가므로 기울기에 아무 연산도 하지 않고 흘러간다. 그리고 곱하기는 매 시각 다른 f와의 아다마르 곱(원소별 곱)이다.
기존 RNN은 계속 같은 행렬을 행렬곱 했었기에 기울기가 폭발하거나 소실됐었다. 그러나 LSTM의 기억 셀은 매번 다른 행렬과 아다마르 곱을 수행하므로 기울기 폭발이나 소실이 일어나기 힘들다.
곱하기는 forget gate와의 곱이므로, 순전파 때 0~1사이의 값이 곱해지는 과정이었다. ‘잊어야 한다’고 판단된 셀에서는 기울기가 작아진채로 역전파된다. 그러나 ‘잊어서는 안된다’라고 판단된 셀에서는 기울기가 작아지지 않고 전파된다.
따라서, 기억 셀이 장기 의존 관계를 유지(학습)할 수 있다.