유튜버 AI Holic님의 ‘Likelihood 쉽게 설명드려요 — 머신러닝, 인공지능을 위한 수학’ 영상을 보고 정리하였음.
확률.
우도에 대해 알아보기 전에, 일단 가장 친숙한 확률이라는 것부터 살펴보자. 고양이들 1,000마리의 몸무게를 재서 다음과 같은 히스토그램 분포가 나왔다고 해보자. 평균은 4, 표준편차는 0.5라고 해보자.
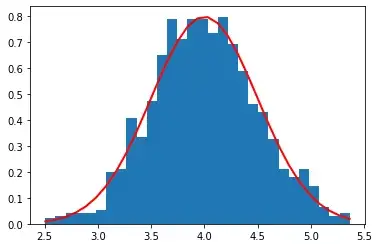
“확률”이란, 다음처럼 우리가 고등학교 때 많이 구하던 바로 그것이다!
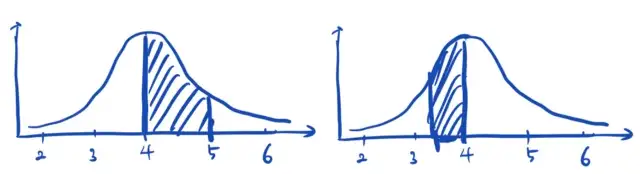
평균은 얼마고, 표준편차는 얼마일 때, 몸무게가 4보다 크거나 같고 5보다 작거나 같을 확률은 얼마인가?
\[\mathbb{P}(4 \le \text{몸무게} \le 5|\mathcal{N}(4, 0.5)) =0.477\]평균은 얼마고, 표준편차는 얼마일 때, 몸무게가 3.5보다 크거나 같고 4보다 작거나 같을 확률은 얼마인가?
\[\mathbb{P}(3.5 \le \text{몸무게} \le 4|\mathcal{N}(4, 0.5)) =0.34\]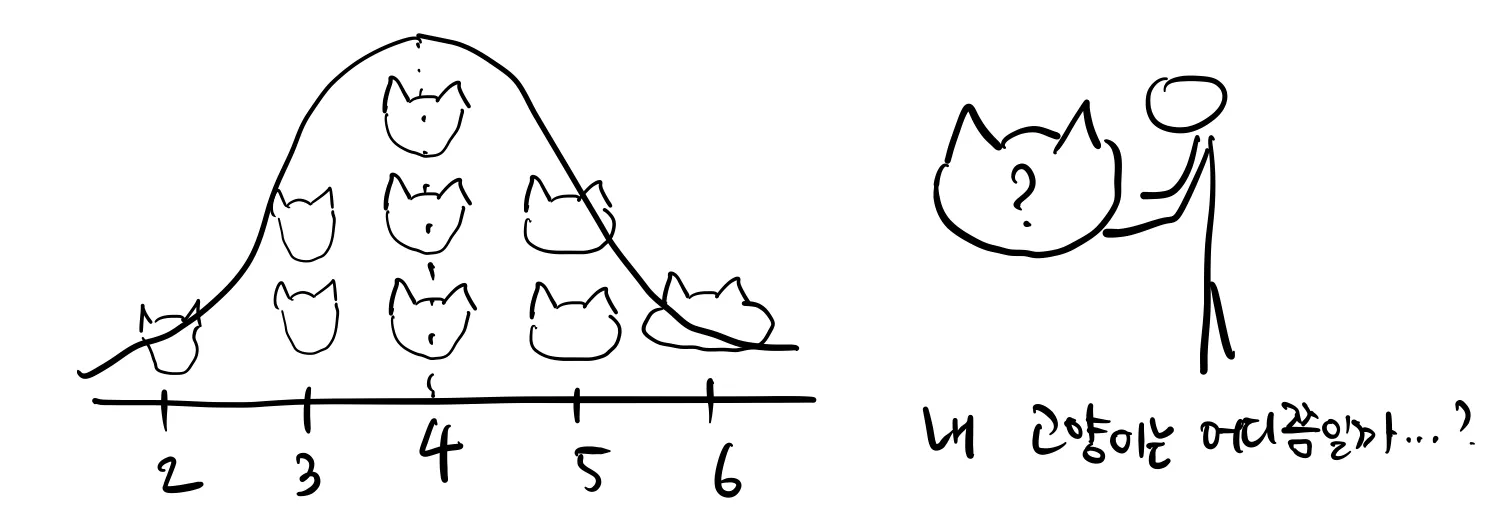
“확률”이란…
사건의 범위는 변하지만, 분포는 고정되어 있는 형태다. 내가 한 마리의 고양이를 키우고 있다고 가정해보자. 위의 분포에서는, 즉, 내가 관측한 고양이들의 몸무게들 중에서는, 내 고양이의 몸무게가 4kg에서 5kg사이일 확률은 47.7%이고, 3.5kg에서 4kg 사이일 확률은 34%이다.
\[\mathbb{P}(\text{data} | \text{distribution})\]보통 “확률”이란, 위와 같은 형태이다. distribution이 정해져 있는 상태에서, 지금 이 데이터가 관측 될 확률이다.
그럼 Likelihood는 무엇일까?
아래 그림을 보자.
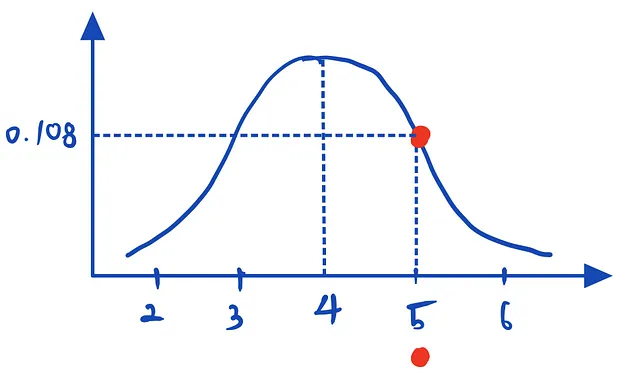
우리집 고양이가 5kg이라고 해보자. (뚱냥이다!)
우리집 뚱냥이의 몸무게라는 데이터(5kg)를 내가 관측했다. 그럼 이 데이터는 어떤 분포로부터 나왔다고 하는 게 가장 말이 될까?
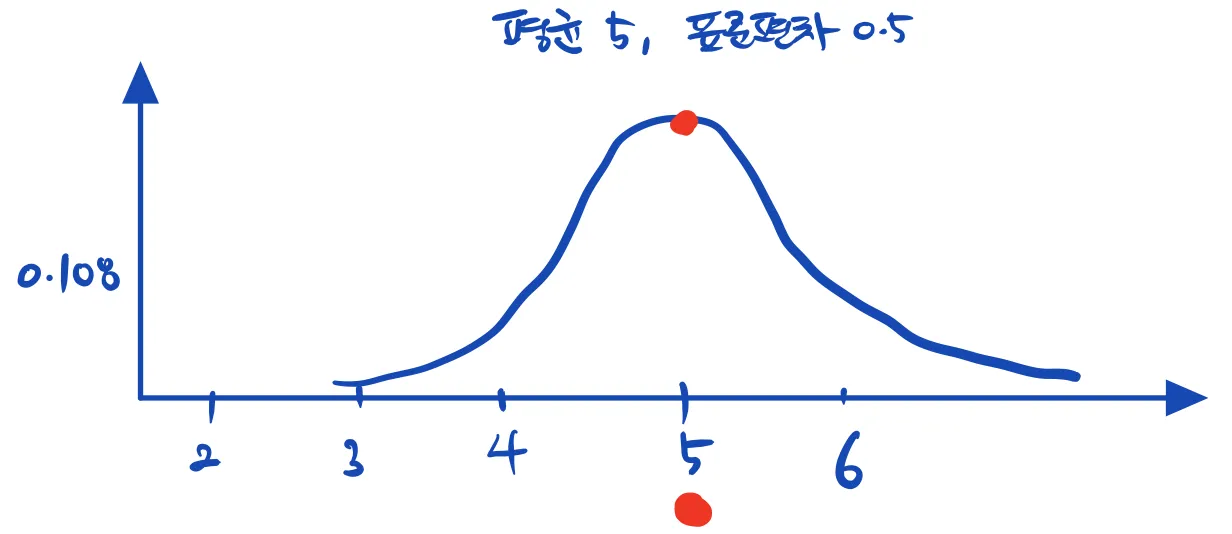
만약 고양이 몸무게의 진짜, 온 세상 모든 고양이의 진리적인 분포가 위 그림처럼 평균 4, 분산 0.5인 정규분포라고 가정해보자. 그럼 이 가정 하에서 우리집 뚱냥이의 likelihood는? 0.108이다.
x=5인 경우의 확률분포의 y절편에 해당한다. 즉, 세로 선의 길이이다.
\[\mathcal{L}(\mathcal{N}(4, 0.5) | \text{고양이몸무게}=5)=0.108\]“고양이 몸무게가 5kg이라고 주어졌을 때, 정규분포 (4, 0.5)의 likelihood는 0.108이다”라고 해석한다.
다시다시, 분포를 오른쪽으로 조금 움직여봅시다!
내 고양이 몸무게가 5kg일 때, 이 데이터가 정규분포(5, 0.5)라는 분포의 likelihood는 0.798이다.
likelihood가 가장 높은 분포를 선택하는 것이 가장 말이 된다는 것은 이해가 간다. 아니 근데, 관측한 데이터로 분포를 때려 맞춘다고 했는데, 그 분포(분포란 평균과 표준편차를 의미함)의 likelihood 계산은 어떻게 하는가?

likelihood
=지금 얻은 데이터(내 뚱냥이 몸무게 = 5kg)가 이 분포로부터 나왔을 가능도
=각 데이터 샘플에서 후보 분포에 대한 높이(likelihood, 기여도)의 곱(iid)
다시다시, 내가 여러 마리의 고양이 몸무게를 측정했다(나는 현재 x들을 알고있다).
그렇다면, 이 몸무게들의 원래 분포는 무엇일까? → \(\theta\)는 무엇일까? → 이 글의 경우에는 정규분포라고 가정했으므로 \(\theta\)가 무엇일까?는 곧 평균과 분산이 무엇일까?가 된다.
→ 이 과정이 바로 최대 우도 추정이다. \(\mathbb{P}(x | \theta)\)가 가장 커지는 \(\theta\)를 추정하는 것이 가장 그럴 듯하다. 즉, 최대 우도 추정이란, \(\mathbb{P}(x | \theta)\)가 가장 커지는 \(\theta\)(여기서는 평균과 표준편차)를 구하는 것이고, 모든 데이터를 이 분포에 빗대어 likelihood를 구해 모두 곱하고, 이 값이 가장 커지는 \(\theta\)를 구하는 과정이다.
똑똑한 누군가는 말한다.
“이 \(\theta\)일 때, 즉 이 분포일 때, 내가 측정한 고양이들의 몸무게 x들이 가장 나옴직해!”