Determinant는 선형 대수에서 중요한 개념이다. Determinant란 선형방정식 시스템의 분석 및 솔루션에 있어서, 수학적인 객체(mathematical object)이다. Determinant는 오직 정방행렬에 대해서만 정의된다. 이 책에서는 determinant를 \(det(A)\) 또는 \(|A|\)로 표기한다.

정방행렬 A의 determinant란 A를 실수로 mapping하는 함수이다. determinant의 정의를 살펴보기 전에, 동기 부여를 위한 예시를 함께 보자.
예제 4.1 (행렬 Invertibility 확인하기)
정방행렬 A가 Invertible(Section 2.2.2)인지 아닌 지를 알아보자. 가장 작은 행렬의 경우 우린 행렬이 invertible일 때를 알고 있다. 만약 \(A\)가 1×1행렬이라면, 즉, 스칼라라면, \(A=a \rightarrow A^{-1}=\frac{1}{a}\)이다. \(a\ne0\)이라면 \(a \times (1/a)=1\)이 성립하기 때문이다. 2×2 행렬이라면, inverse의 정의(Definition 2.3)에 의해 \(AA^{-1}=I\)인 것을 알고 있다. 그러면 2.24와 함께 \(A\)의 inverse는 다음과 같다.
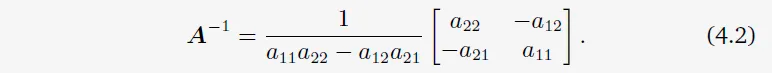
그러므로, \(a_{11}a_{22}-a_{12}a_{21} \ne 0\) (4.3)이라면 \(A\)는 invertible하다. 바로 \(a_{11}a_{22}-a_{12}a_{21}\)라는 이 수가 2×2 행렬 A의 determinant이다. 즉, 다음과 같다.
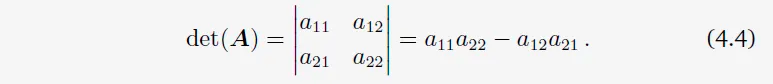
예제 4.1은 determinant와 역행렬 존재 여부 사이의 관계를 나타낸다. 다음 theorem은 n × n 행렬에 대해 동일한 결과를 명시합니다.
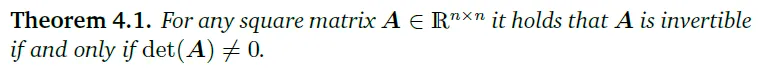 어느 정방행렬 A에 대하여, \(det(A)\ne0\)라면 A는 invertible하다.
어느 정방행렬 A에 대하여, \(det(A)\ne0\)라면 A는 invertible하다.
작은 행렬들에 대해서는 determinant의 명확한 표현이 존재한다. \(n=1\)일 때,
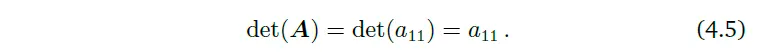
\(n=2\)일 때,
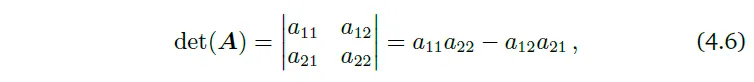
이는 앞선 예제에서 살펴본 바와 같다.
\(n=3\)일 때 Sarrus’ rule은 다음과 같다.
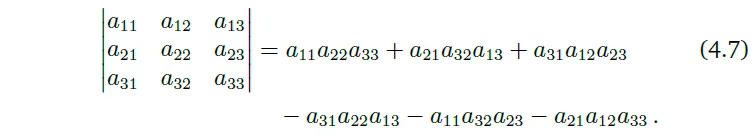
Sarrus’ rule의 곱셈항을 기억하기 위해서는 행렬 안의 세 가지씩 곱한 요소들을 잘 추적해야한다.
\(i>j\)에 대하여 \(T_{ij}=0\)라면 정방행렬 \(T\)를 upper-triangular matrix라고 한다. 즉, 이 행렬은 대각선 밑으로는 0이다. 비슷하게, lower-triangular matrix를 대각선 위가 0인 행렬로 정의한다. 이와 같은 triangular 행렬 \(n × n\)의 \(T\)에 대하여, determinant는 대각 element들의 곱이다.
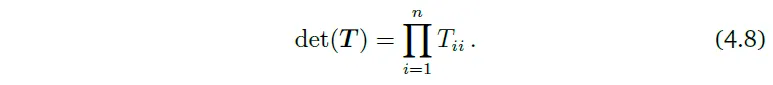
예제 4.2 (부피 측정 수단으로서의 determinants)
determinant의 개념을 보면, 우리는 이를 \(\mathbb{R}^n\)에서 어느 객체를 span하는 n개의 벡터들을 매핑하는 것으로 바라봐도 자연스럽다. 행렬 \(A\)의 determinant인 \(det(A)\)가 \(A\)의 column들로 형성되는 n차원의 평행 육면체의 부호를 가진 부피인 것이 알려져 있다. \(n=2\)일 때, 행렬의 각 column들은 평행사변형을 형성할 수 있다; Figure 4.2를 보자.
 Fiture 4.2 벡터 b와 g에 의해 span되는 평행사변형의 넓이(그림자 진 지역)는 \(|det([b,g])|\)이다.
Fiture 4.2 벡터 b와 g에 의해 span되는 평행사변형의 넓이(그림자 진 지역)는 \(|det([b,g])|\)이다.
벡터들 사이의 각도가 작아질수록, 평행사변형의 넓이 또한 줄어든다. 두 벡터 \(\boldsymbol{b}\), \(\boldsymbol{g}\)가 행렬 \(A\)의 column이라고 생각해보자. \(A=[\boldsymbol{b}, \boldsymbol{g}]\)이다. 그럼 \(A\)의 determinant의 절댓값은 꼭지점 0, \(\boldsymbol{b}\), \(\boldsymbol{g}\), \(\boldsymbol{b}+\boldsymbol{g}\)로 이루어진 평행사변형의 넓이이다. 만약 \(\boldsymbol{b}\)와 \(\boldsymbol{g}\)가 linearly dependent이어서 \(\boldsymbol{b}=\lambda \boldsymbol{g}\)라면(\(\lambda \in \mathbb{R}\)), 이들은 더 이상 2차원 평행사변형을 형성하지 않을 것이다. 그러므로 그때의 넓이는 0이다. 반대로, 만약 \(\boldsymbol{b}\), \(\boldsymbol{g}\)가 linearly independent이고 각각이 canonical basis 벡터 \(\mathbf{e}_1\), \(\mathbf{e}_2\)의 배수라면, 이들은 다음과 같이 쓰여질 수 있다.
\[\boldsymbol{b} = \begin{bmatrix} b \\ 0 \end{bmatrix}\] \[\boldsymbol{g} = \begin{bmatrix} 0 \\ g \end{bmatrix}\]그러면 determinant는 다음과 같다.
\[\begin{vmatrix} b & 0 \\ 0 & g \end{vmatrix}\]determinant의 부호는 \(\boldsymbol{b}\), \(\boldsymbol{g}\)의 standard basis (\(\mathbf{e}_1\), \(\mathbf{e}_2\))에 대한 방향을 나타낸다. 우리의 그림에서는 \(\boldsymbol{g}\), \(\boldsymbol{b}\)로 뒤집는 것이 \(A\)의 column을 서로 바꾸고 그늘 진 지역의 방향을 역방향으로 바꾸는 것과 동일해진다. 이것이 바로 우리에게 친숙한 공식, ‘넓이=높이×길이’이다. 이는 더 높은 차원으로도 이어진다. \(\mathbb{R}^3\)에서는, 평행 육면체의 모서리를 span하는 세 가지 벡터 \(\boldsymbol{r}, \boldsymbol{b}, boldsymbol{g} \in \mathbb{R}^3\)를 고려해보자. 즉, 마주보는 면이 평행한 평행 육면체인 것이다. Figure 4.3을 보자.
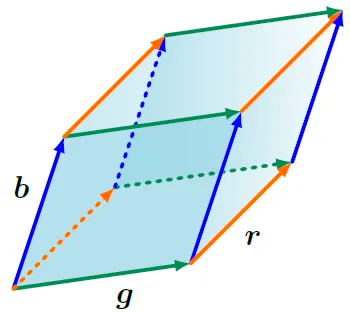 Figure 4.3 세 벡터 r, g, b에 의해 span되는 평행육면체의 부피는 |det([r, b, g])|이다. determinant의 부호는 span중인 벡터들의 방향을 나타낸다.
Figure 4.3 세 벡터 r, g, b에 의해 span되는 평행육면체의 부피는 |det([r, b, g])|이다. determinant의 부호는 span중인 벡터들의 방향을 나타낸다.
3×3 행렬 \([\boldsymbol{r}, \boldsymbol{b}, \boldsymbol{g}]\)의 determinant의 절댓값은 도형의 부피이다. 그러므로, determinant는 행렬을 구성하는 column 벡터들에 의해 형성되는 부호 있는 부피를 측정하는 함수로서 역할한다. 세 선형 독립 벡터 \(\boldsymbol{r}, \boldsymbol{b}, \boldsymbol{g} \in \mathbb{R}^3\)이 다음과 같이 주어졌다고 해보자.
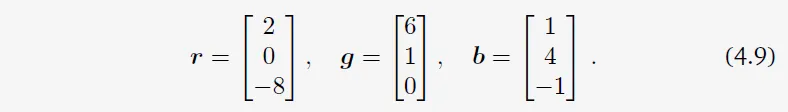
이 벡터들을 행렬의 column으로 쓰는 것은 원하는 볼륨을 계산할 수 있도록 해준다.
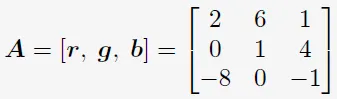
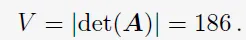
\(n×n\) 행렬의 determinant를 계산하는 것은 \(n>3\)인 케이스를 풀기 위한 일반적인 알고리즘을 요구한다. 이 경우에는 다음과 같이 살펴보자. Theorem 4.2는 \(n\times n\)행렬의 determinant를 계산하는 일을 \((n-1)\times(n-1)\) 행렬의 determinant를 계산하는 문제로 축소시킨다. Laplace expansion (Theorem 4.2)을 재귀적으로 적용함으로써, 결과적으로는 \(2\times2\) 행렬의 determinant를 계산함으로써 \(n\times n\) 행렬의 determinant를 계산할 수 있다.
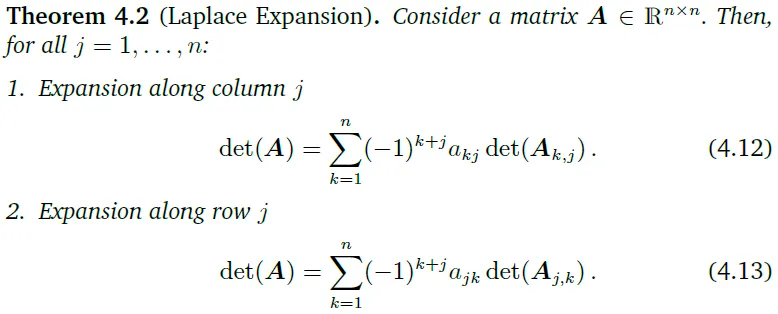
\(A_{k, j} \in \mathbb{R}^{(n-1)\ times (n-1)}\)는 \(A\)행렬에서 \(k\)행과 \(j\)열을 삭제하여 얻을 수 있는 submatrix이다.
예제 4.3 (Laplace Expansion) 첫 번째 row을 따라 Laplace expansion을 적용해가며 아래와 같은 행렬 \(A\)의 determinant를 계산해보자.
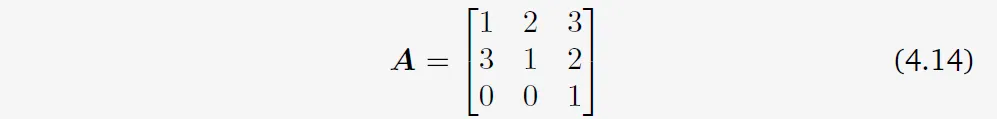
식 4.13을 적용하면 결과는 다음과 같다.
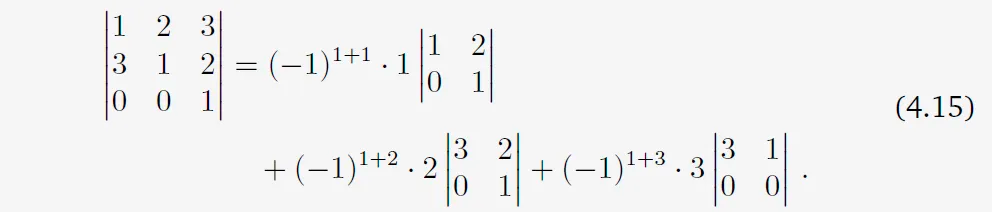
식 4.6을 이용해서 모든 \(2 \times 2\) 행렬의 determinant를 계산하고, 아래와 같은 답을 얻을 수 있다.
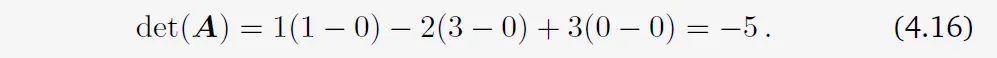
위 결과를 Sarru’s rule을 이용해서 구한 결과와 비교해보자.
행렬 \(A \in \mathbb{R}^{(n \times n)}\)에 대한 determinant를 아래와 같은 특성을 가진다.
- 행렬곱의 determinant는 각각의 determinant의 곱과 같다. \(det(AB)=det(A)det(B)\).
- 전치(Transposition)를 해도 determinant는 변하지 않는다. 즉, \(det(A)=det(A^T)\).
- 만약 \(A\)가 regular하다면 (invertible하다면), \(det(A^T)=\frac{1}{det(A)}\)이다.
- Similar 행렬(Definition 2.22)들은 determinant가 같다. 그러므로, linear mapping \(\Phi: V \rightarrow V\)에 대한 \(\Phi\)의 모든 transformation 행렬 \(A_\Phi\)의 determinant는 모두 같다. 그러므로, linear mapping의 basis를 어떻게 선택한다해도 determinant는 변하지 않는다.
- 여러 개의 행/열을 다른 것에 더하는 것은 \(det(A)\)를 변화시키지 않는다.
- 행/열에 \(\lambda \in \mathbb{R}\)을 곱하는 것이면 \(det(A)\)도 \(\lambda\)만큼 곱해진다. 특히, \(det(\lambda A)=\lambda^n det(A)\)이다.
- 두 행/열을 뒤바꾸는 것은 \(det(A)\)의 부호를 변화시킨다.
마지막 세 가지의 특성때문에 가우시안 소거법(Gaussian elimination)(Section 2.1)을 이용해 \(det(A)\)를 계산할 수 있다. 바로 \(A\)를 row-echelon form으로 변환함으로써 말이다. \(A\)가 triangular form이 될 때까지 수행하면 된다. 즉 \(A\)의 대각 요소 아래 쪽이 모두 0이면 된다. 식 4.8을 다시 생각해보자. triangular 행렬의 determinant는 대각 요소들의 곱이었다.
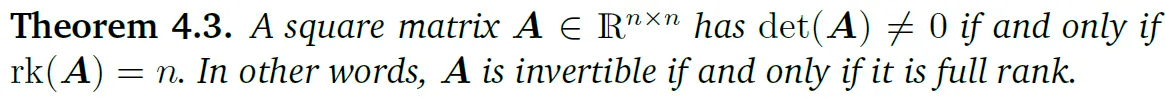 정방 행렬 \(A \in \mathbb{R}^{n \times n}\)이 있을 때, \(rk(A)=n\)이라면 \(det(A) \ne 0\)이다. 즉, \(A가\) full rank라면 A는 invertible하다.
정방 행렬 \(A \in \mathbb{R}^{n \times n}\)이 있을 때, \(rk(A)=n\)이라면 \(det(A) \ne 0\)이다. 즉, \(A가\) full rank라면 A는 invertible하다.
수학이 주로 손으로 쓰여졌던 시절에는 행렬의 invertibility를 알아내기 위하여 determinant 계산이 필수적이었다. 그러나, 머신러닝 분야에서의 현대적인 접근은 바로 직접적인 숫자적 방법을 사용하는 것이다. 이것이 determinant를 하나하나 계산하는 것을 대체할 수 있다. 예를 들면, 챕터 2에서 우리는 가우시안 소거법으로 역행렬을 구하는 방법을 배웠었다. 그러므로 가우시안 소거법은 행렬의 determinant를 계산하는데에 사용될 수 있다.
Determinant는 다음 섹션에서 이론적으로 중요한 역할을 한다. 특히 특성 방정식(characteristic polynomial)을 이용해 eigenvalues와 eigenvectors를 배울 때 그렇다.
Definition 4.4. 정방행렬 \(A \in \mathbb{R}^{n \times n}\)의 trace는 아래와 같이 정의된다.
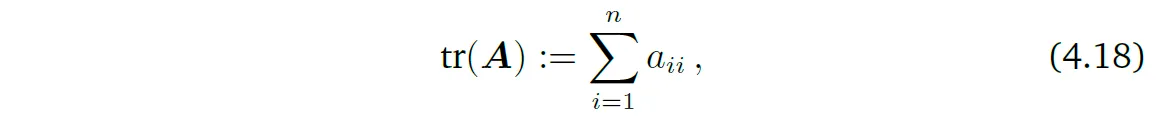
즉, trace는 \(A\)의 대각 요소들의 합이다.
trace는 다음과 같은 특성들을 만족한다:
- \[tr(A+B)=tr(A) + tr(B) \text{for} A, B \in \mathbb{R}^{n \times n}\]
- \[tr(\alpha A) = \alpha tr(A), \alpha \in \mathbb{R} \text{for} A \in \mathbb{R}^{n \times n}\]
- \[tr(I_n)=n\]
- \[tr(AB)=tr(BA) \text{for} A \in \mathbb{R}^{n \times k}, B \in \mathbb{R}^{k \times n}\]
trace의 행렬곱에 대한 특성들은 좀 더 일반적이다. 특히, trace는 cyclic permutations에 invariant하다. 즉, 행렬 \(A \in \mathbb{R}^{a \times k}, K \in \mathbb{R}^{k \times l}, L \in \mathbb{R}^{l \times a}\)에 대하여
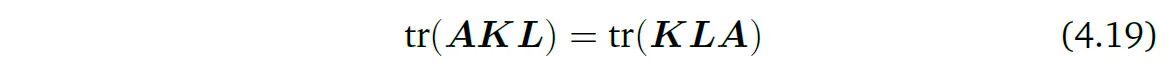
식을 만족한다. 이 특성은 행렬이 임의의 개수여도 적용된다. 식 (4.19)의 특별한 경우로, 두 벡터 \(x, y \in \mathbb{R}^n\)에 대하여 다음과 같다.
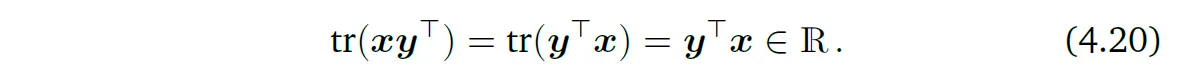
\(V\)가 벡터 공간이라 하고 linear mapping \(\Phi : V \rightarrow V\)가 주어졌을 때, \(\Phi\) 행렬의 trace를 사용하여 이 매핑의 trace를 정의할 수 있다. \(V\)의 basis가 주어졌을 때, transformation 행렬 \(A\)를 이용하여 \(\Phi\)를 설명할 수 있다. 그러면 \(\Phi\)의 trace는 \(A\)의 trace이다. \(V\)의 basis가 달라진다면, \(\Phi\)에 대응하는 transformation 행렬 \(B\)는 적절한 \(S\)에 대한 \(S^{-1}AS\)처럼 basis를 바꿈으로써 얻어질 수 있다(Section 2.7.2). \(\Phi\)의 대응하는 trace에 대하여, 다음과 같다.
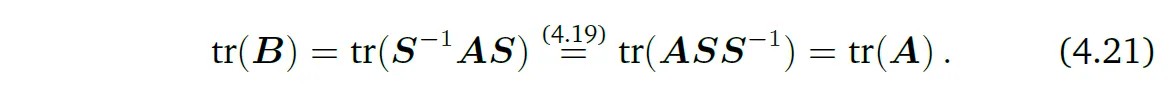
그러므로, linear mapping의 행렬 표현이 basis에 dependent한 반면 linear mapping Φ의 trace는 basis에 independent하다.
이번 섹션에서는 정방 행렬을 특성화하는 함수로서의 determinant와 trace에 대해 다뤘다. 이 두 가지에 대한 이해를 바탕으로 이제는 행렬 \(A\)를 설명하는 중요한 식을 특성 다항식의 관점에서 정의할 수 있다. 이는 다음 섹션에서 광범위하게 다뤄질 것이다.
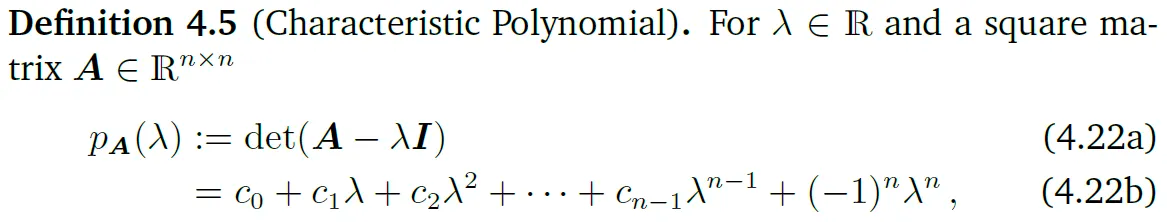
이 때 \(c_0, \cdots, c_{n-1} \in \mathbb{R}\)이며, 위 식은 \(A\)의 특성방정식이라고 불린다. 특히,
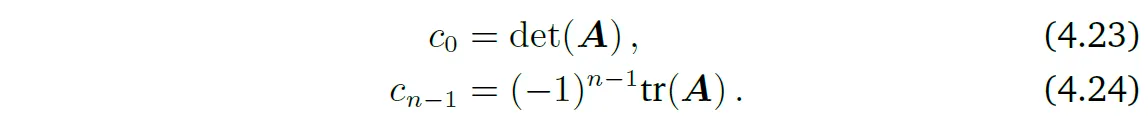
를 만족한다. 특성 방정식(4.22a)는 다음 섹션에서 다룰 eigenvalue와 eigenvector를 계산하도록 도와준다.
끝! 다음은 4.2 Eigenvalues and Eigenvectors.
본 게시글은 ‘Mathematics of Machine Learning’ 책을 번역하였습니다. 한 호흡에 읽히도록, 복습 시 빨리 읽히도록 적어 놓는 것이 이 글의 목적입니다.