논문 링크 : E commerce in Your Inbox Product Recommendations at Scale
제안된 방법은 이전 구매 내역(이메일로 날라온 영수증)을 이용하여 그 영수증 안의 상품들을 학습하여 추천하는 방법이다. Prod2vec을 발전시킨 Meta-prod2vec이 네이버 상품 추천시스템 중 유사아이템 추천시스템에 참고되었다(2021 DEVIEW).
제안된 방법은 상품을 저차원 공간에서의 표현(representation)으로 학습하는 방법을 제안한다. 임베딩 공간 안에서 최근접 이웃을 찾음으로써 추천이 이루어진다.
\(\mathcal{S}\)는 이메일 영수증들의 집합으로써, N명의 유저로부터 얻어진 것이다. 유저의 로그는 \(s=(e_1, e_2, …, e_M)\)으로 구성되며 \(s \in \mathcal{S}\)이다. 각각의 이메일 e는 \(T_m\)개의 상품들 p로 구성되어있음. 즉, \(e_m = (p_{m_1}, p_{m_2}, …, p_{m_{T_m}})\)이다.
목적 : 각각의 상품 p의 D차원 표현인 \(\mathbf{v}_p\)를 찾는 것. 이 때 당연하지만 유사한 아이템은 근처에 위치해야함.
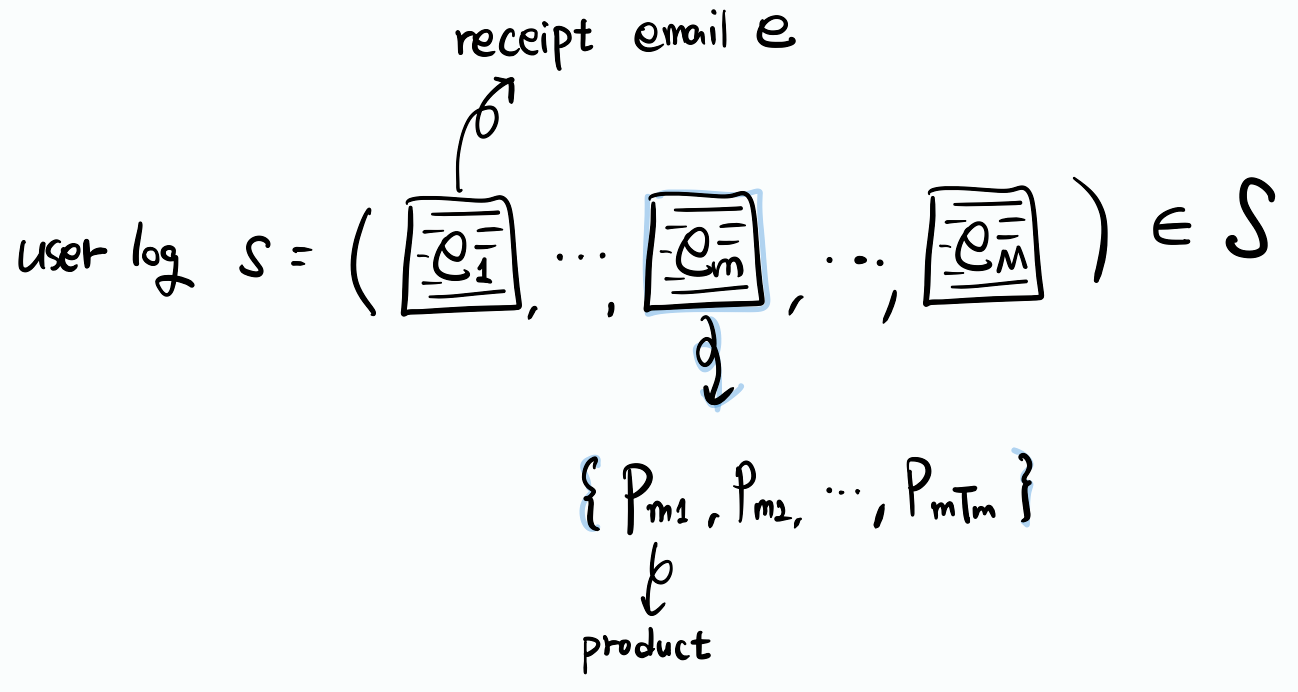 s는 이메일(e)의 시퀀스이며, 이메일은 product로 구성되어있다.
s는 이메일(e)의 시퀀스이며, 이메일은 product로 구성되어있다.
저차원의 상품 임베딩
prod2vec
prod2vec 모델은 NLP 분야에서의 용어를 빌리자면 구매 시퀀스를 문장으로, 시퀀스 안의 상품들을 단어로 보고 상품의 벡터 표현을 학습하는 것이다. 본 논문에서는 Skip-gram 방식[24]을 사용하였다. 그리하여 아래의 목적함수를 최대화시킨다. 목적함수란 만약 사각형을 가장 크게 만들고 싶다고 가정할때 사각형의 넓이같은 것을 의미한다. MLE가 대표적인 목적함수이다.
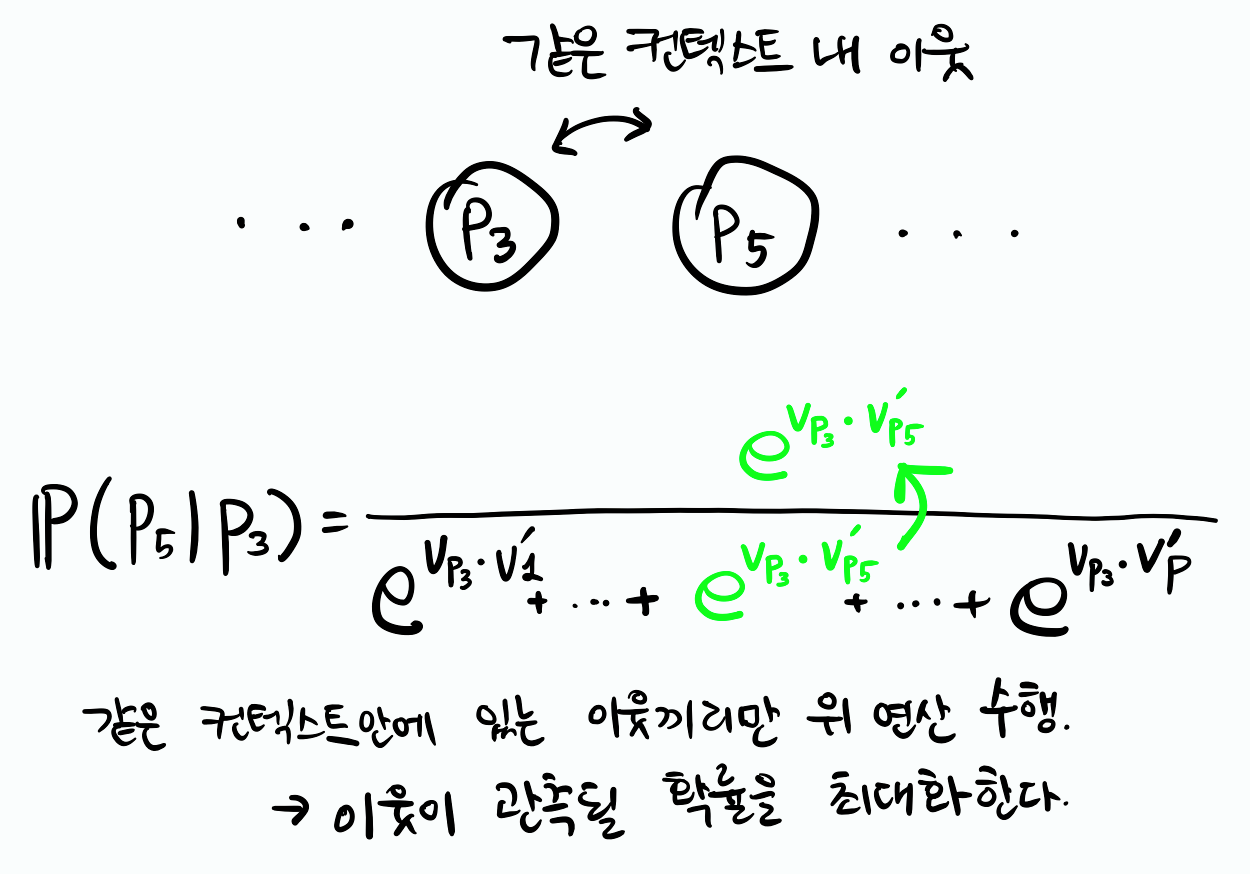
\[\mathcal{L} = \sum_{s \in \mathcal{S}} \sum_{p_i \in s} \sum_{-c \le j \le c, j \ne 0} \log \mathbb{P}(p_{i+j} \mid p_i) \tag{3.1}\]같은 \(s\) 안에 있는 상품들은 임의로 배열된다. \(\mathbb{P}(p_{i+j} \mid p_i)\)는 상품 \(p_i\)가 주어졌을 때 이웃하는 상품 \(p_{i+j}\)를 관측할 확률이며 아래와 같이 소프트맥스 함수로 정의된다.
\[\mathbb{P}(p_{i+j} \mid p_i) = \frac{\exp (\mathbf{v}^T_{p_i} \mathbf{v}'\_{p_{i+j}})} {\sum_{p=1}^{P} \exp( \mathbf{v}^T_{p_i} \mathbf{v}'_p)} \tag{3.2}\]\(\mathbf{v}_p\)는 인풋, \(\mathbf{v}'_p\)은 아웃풋 벡터 표현을 의미한다. c는 컨텍스트의 길이이다. P는 단어의 수이다.
bagged-prod2vec
다수의 상품이 동시에 구매되었다는 정보를 고려하기 위해 skip-gram모델을 변형한 모델이다. 쇼핑백의 개념을 도입한다. 이 모델은 상품 수준이 아니라 영수증 수준에서 동작한다. 상품 벡터 표현은 아래와 같이 변형된 목적함수를 최대화함으로써 얻어진다.
\[\mathcal{L} = \sum_{s \in \mathcal{S}} \sum_{e_m \in s} \sum_{-n \lt j \lt n, j \ne 0} \sum_{k=1, \cdots , T_m} \log \mathbb{P}(e_{m+j} \mid p_{mk}) \tag{3.3}\]prod2vec(수식 3.1)과의 차이는 j가 상품 수준에서 영수증 수준으로 바뀌었다는 것이다. 다른 컨텍스트의 아이템과 연산.
\(\mathbb{P}(e_{m+j} \mid p_{mk})\)는 이웃하고 있는 영수증 \(e_{m+j}\)를 관측할 확률이다. 영수증 \(e_{m+j}\)는 상품으로 구성되어 있으므로 \(e_{m+j} = (p_{m+j}, \cdots, p_{m+j, T_m})\)이다. 상품 \(p_{mk}\)가 주어졌을 때 왜 한 단계 더 높은 수준인 영수증을 관측할 확률인가 헷갈릴 수도 있지만, \(\mathbb{P}(e_{m+j} \mid p_)\)는 다음과 같다.
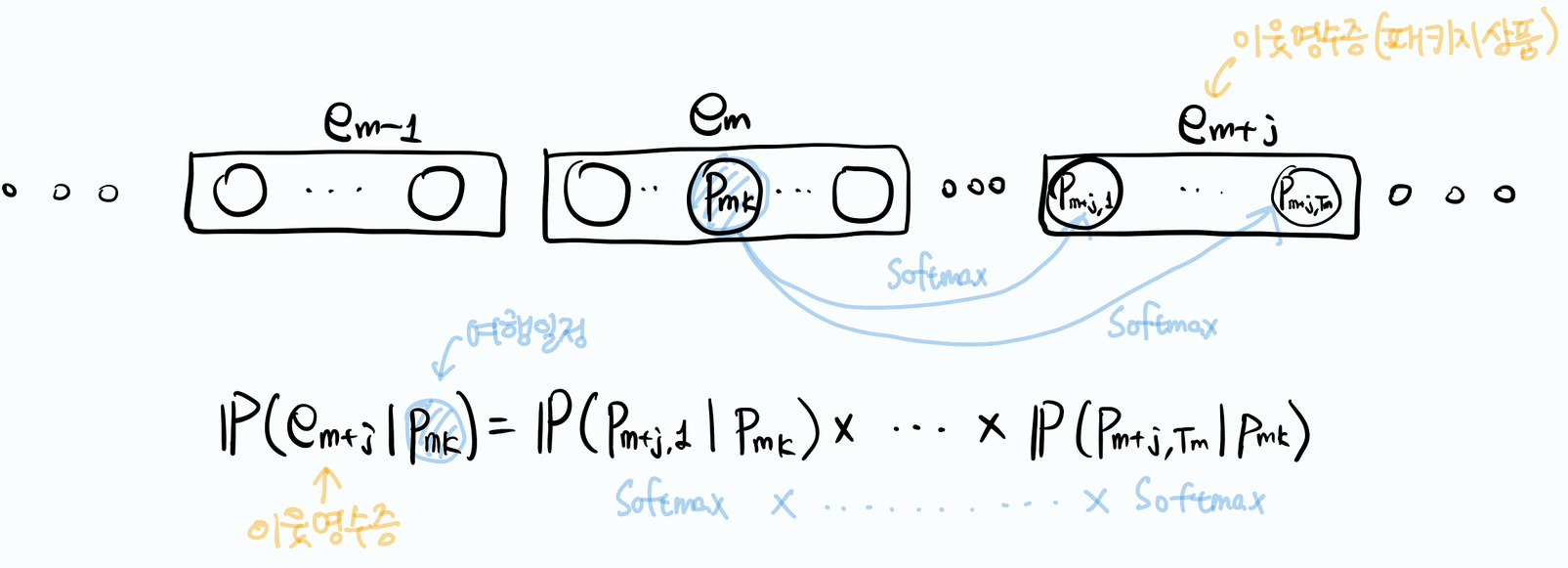
상품 구매의 시간적 정보를 반영하기 위해서 directed 언어 모델을 제안했다. 이는 컨텍스트로서 미래의 상품만 사용하겠다는 것이다[12]. 위처럼 수정함으로써 상품 임베딩값은 미래 있을 구매 여부를 예측할 수 있도록 학습된다.
상품-to-상품 예측 모델
저차원의 상품 표현을 학습하고 난 후 다음으로 구매 할 아이템을 예측하는데 있어 몇 가지 방법이 있다.
prod2vec-topK
구매한 상품이 주어지면, 모든 다른 상품들과 코사인 유사도를 계산해서 가장 유사한 top K 아이템을 추천함.
prod2vec-cluster
추천의 다양성을 위해 상품들을 여러 클러스터들로 그룹핑하고, 이전에 구매한 상품이 속해있는 클러스터와 가장 연관 있는 클러스터 내의 상품을 추천한다. K-means 클러스터링을 썼으며, 상품 표현들 사이의 코사인 유사도를 기반으로 그룹핑했다. \(C\)개의 클러스터가 있다고 하자. \(c_1\)라는 클러스터에서 구매가 일어난 후 다음 구매는 Multinomial distribution \(\theta_{i1}, \theta_{i2}, \cdots, \theta_{iC}\)를 따른다. \(\theta_{ij}\)는 \(c_i\)에서 구매가 일어난 다음 \(c_j\)에서 구매가 일어날 확률이며 다음과 같다.
\[\hat{\theta}_{ij} = \frac{\text{# of times } c_i \text{ purchase was followed by } c_j}{\text{count of } c_j \text{ purchased}} \tag{3.4}\]구매했던 상품 \(p\)가 주어졌다 -> \(p\)가 어느 클러스터에 속하는지 확인 -> \(p\)가 만약 \(c_i\)라는 클러스터에 속해있다면 \(c_i\)와 가장 연관된 클러스터를 여러개 찾음 -> 그 속의 상품들과 \(p\)와 코사인 유사도를 계산하여 상위 K개를 추천한다.