Neural graph collaborative filtering(2019) 논문의 Methodology 부분을 다룹니다. 논문에서 Methodology에 대한 설명은 크게 세 부분으로 구성되어 있습니다.

pytorch 코드 : huangtinglin/NGCF-PyTorch

Embedding Layer
Embedding Propagation Layers
1. First-order propagation
2. High-order propagation
Model Prediction
Optimization

1. Embedding Layer

메인스트림 추천모델인 Unifying Knowledge Graph Learning and Recommendation, NCF, BPR에 따르면, 유저 \(u\)(아이템 \(i\))는 임베딩 벡터 \(\mathbf{e}_u \in \mathbb{R}^d(\mathbf{e}_i \in \mathbb{R}^d)\)로 나타낸다. 즉 \(d\)차원의 임베딩 벡터로.

MF나 NCF같은 기존 모델은 임베딩을 바로 interaction layer로 전달하여, 즉 바로 내적하거나 신경망에 전달해서 예측 스코어를 계산합니다. 하지만 NGCF는 유저-아이템 그래프 상에서 propagating하여 임베딩을 정교화(refine이라고 표현)합니다. 이걸 임베딩 정교화(embedding refinement) step이라고 하는데, 이 과정을 통해 collaborative signal을 임베딩에 주입할 수 있기 때문이라고 합니다.

2. Embedding Propagation Layers

GNN의 message-passing 아키텍쳐를 이용하여 그래프 구조를 따라 CF 시그널을 잡아내고 유저-아이템 임베딩을 정교화합니다. 우선 하나의 레이어에서 어떻게 전파가 이루어지는지 확인하고, 여러 레이어로 확장해봅시다.

1. First-order propagation

직관적으로 봤을 때, 어느 유저에 의해 사용된(클릭된) 아이템은 해당 유저의 선호도를 구성할 수 있습니다. 마찬가지로, 특정 아이템을 사용한 유저들은 해당 아이템의 특징을 구성하고 있습니다. 또한 두 아이템의 유사도를 측정하는데 사용될 수도 있을 겁니다. 이러한 가정을 기반으로, 상호작용한 유저와 아이템 사이에 임베딩 전파를 수행합니다. 이 때, message construction과 message aggregation이라는 개념이 사용됩니다.

Message Construction

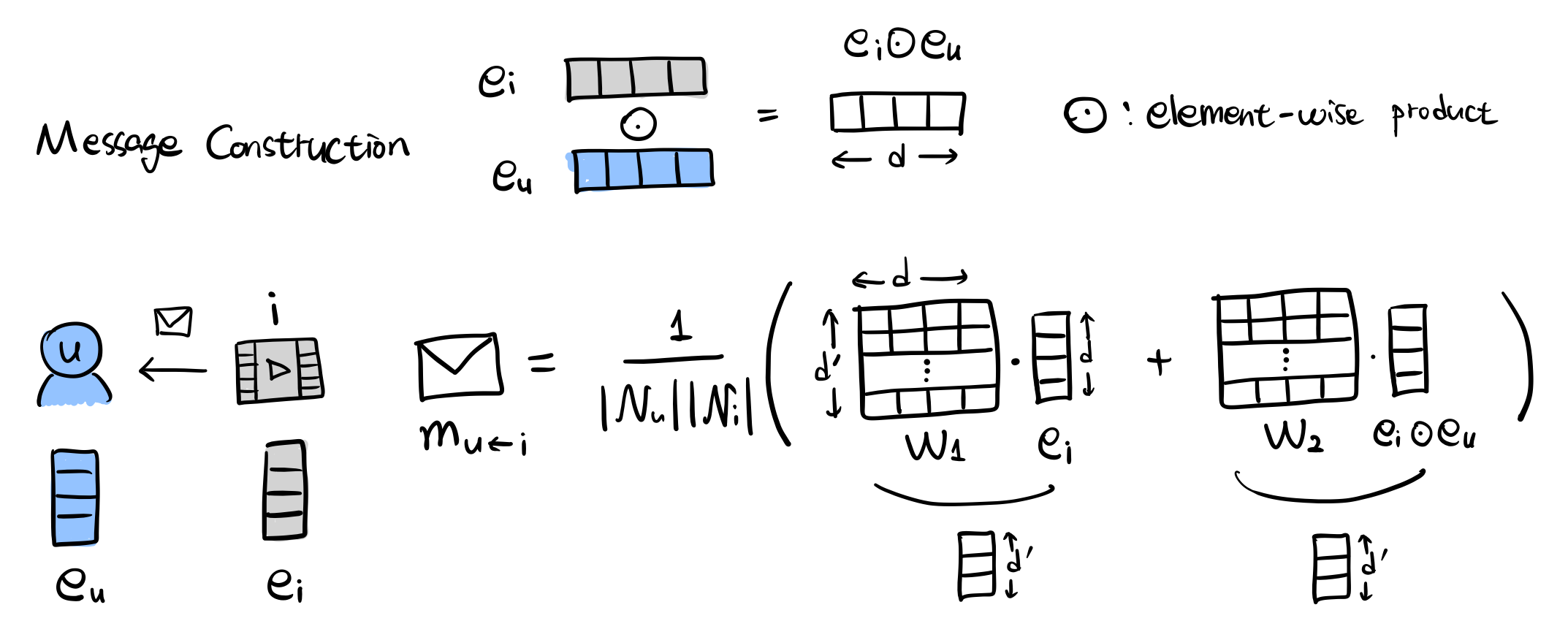
서로 연결된 유저-아이템 쌍 \((u, i)\)에 대하여, \(i\)에서 \(u\)로의 message를 다음과 같이 정의합니다.

\[m_{u \leftarrow i} = f(e_i, e_u, p_{ui})\]

\(m_{u \leftarrow i}\)는 메시지 임베딩, 즉 전파되는 정보를 의미합니다. \(f(\cdot)\)는 메시지 인코딩 함수라고 하며, 임베딩 \(e_i\) 와 \(e_u\), 그리고 \(\text{edge}(u, i)\)의 전파에 대한 감쇠인자(decay factor)를 조정하기 위한 계수 p_{ui}를 인풋으로 받습니다.

본 논문에서는 \(f(\cdot)\)을 다음과 같이 정의합니다:

\[m_{u \leftarrow i} = \frac{1}{\sqrt{|N_{u}||N_i|}}(W_1 \textbf{e}_i + W_2(e_i \odot e_u))\]

\(W_1, W_2 \in \mathbb{R}^{d' \times d}\)는 학습 가능한 가중치 행렬입니다. 이 행렬은 전파라는 것이 유용한 정보를 추출(또는 정제, distill)합니다. 전통적인 Graph convolutional networks( 2016.Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering., 2017. Semi-Supervised Classification with Graph Convolutional Networks., 2017. Graph Convolutional Matrix Completion., 2018. Graph Convolutional Neural Networks for Web-Scale Recommender Systems. )에서는 메시지에 오직 \(e_i\)의 contribution만 고려됐었습니다. 하지만 NGCF는 \(e_i\)와 \(e_u\)사이의 상호작용을 \(\mathbf{e}_i \odot \mathbf{e}_u\)라는 (element-wise product) 형태로 메시지에 추가로 인코딩해줍니다. 이는 \(\mathbf{e}_i\)와 \(\mathbf{e}_u\) 사이의 유사성(또는 관련성, affinity)에 메시지가 의존하게 되죠. 예를 들어, 유사한 아이템 아이템들과는 \(\odot\) 값도 클 테니 유사한 아이템들의 정보를 더 많이 받게 되겠죠. 이는 모델의 표현 능력(representation ability)도 향상시킬 수 있고 자연히 추천 성능도 향상된다고 합니다. (증명은 실험 부분에서 한다고 하네요)

2017. Semi-Supervised Classification with Graph Convolutional Networks.처럼, 여기서는 graph Laplacian norm이라는 개념을 \(p_{ui}=\frac{1}{\sqrt{|N_u||N_i|}}\)을 도입합니다. 여기서 \(N_u\)과 \(N_u\)는 각각 유저 \(u\)와 아이템 \(i\)의 first-hop 이웃을 나타냅니다. representation 학습의 관점에서 보면, \(p_{ui}\)는 아이템 \(i\)가 유저 \(u\)의 선호도에 얼만큼 공헌했는지를 의미합니다. 아이템 \(i\)를 소비한 유저가 많다면, 그 중 한 유저에게 보내는 메시지는 영향력이 적겠죠? 유저 입장에서도 마찬가지입니다. 유저 \(u\)가 아주 많은 아이템을 소비했다면, 그 중 특정 아이템 \(i\) 사이의 메시지 \(m_{u \leftarrow i}\)의 영향력이 줄어드는 것이 맞겠죠.

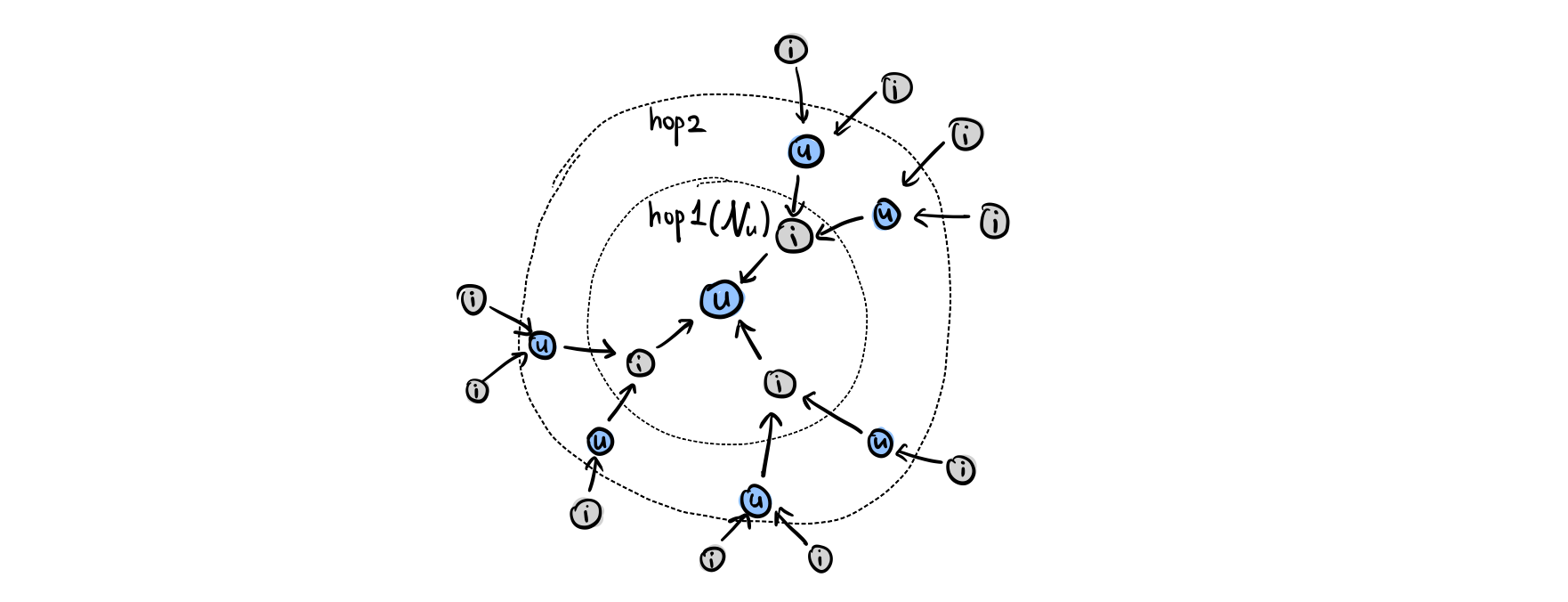
한편 메시지 패싱 관점에서는 \(p_{ui}\)를 감쇠 인자로 해석됩니다. 즉, 경로의 길이가 길어짐에 따라 공헌도가 감소해야 한다는 것을 반영합니다.

Message Aggregation

이제 유저 \(u\)의 이웃으로부터 전파되는 메시지들을 결합함으로써 \(u\)의 표현을 정교화(refine)합니다. Aggregation의 함수는 다음과 같습니다:

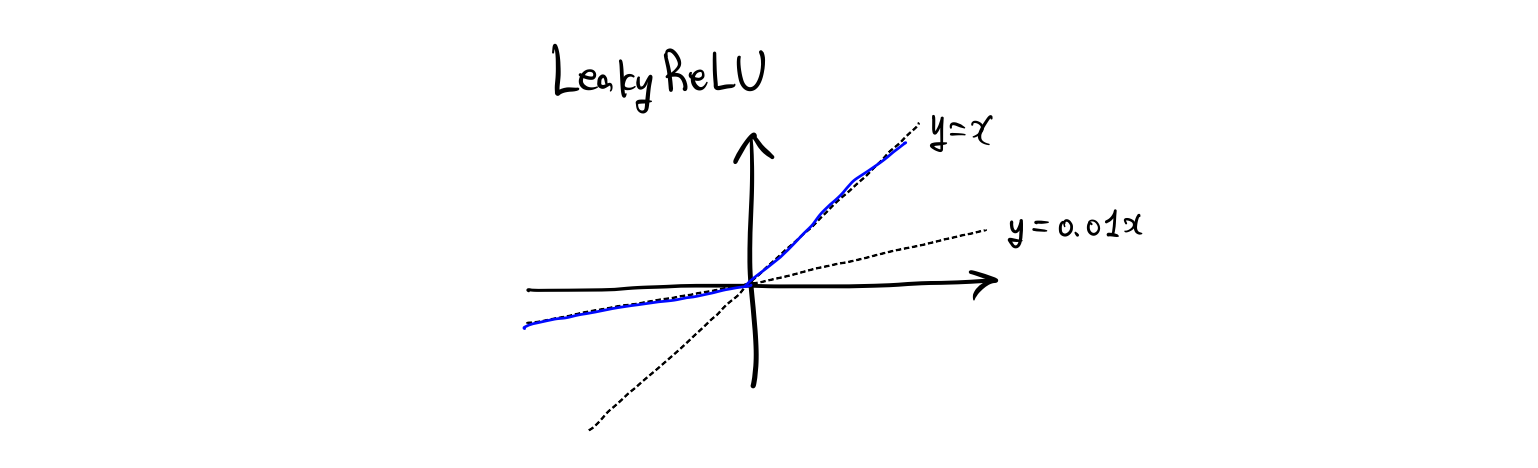
\[e_u^{(1)} = \text{LeakyReLU}(m_{u \leftarrow u} + \sum_{i \in N_u} m_{u \leftarrow i})\]

\(e_u^{(1)}\)은 유저 \(u\)의 representation인데, 위첨자 \(^{(1)}\)은 첫 번째 임베딩 전파 레이어 이후 얻은 것을 의미합니다. 활성화 함수로 쓰이는 LeakyReLU는 양수가 들어오는 경우 그대로 통과시키고 음수는 0.01을 곱한 값을 내놓는 함수입니다. 주목할 점은 이웃 \(N_u\)로부터 전파된 메시지들 뿐만 아니라, 유저 \(u\)의 self-connection \(m_{u \leftarrow u}=W_1e_u\)을 고려했다는 것입니다. \(m_{u \leftarrow u}\)는 원본 특징(original feature)의 정보를 보유하고 있습니다. \(W_1\)은 \(m_{u \leftarrow i}\)에서 쓰였던 \(W_1\)과 동일한 가중치 행렬입니다. 같은 행렬이 다시 한 번 쓰이는 것입니다. 유사하게, 아이템 \(i\)에 대한 표현 \(e_i^{(1)}\)도 얻을 수 있습니다. 이 때는 연결된 유저들로부터의 정보를 전파하면 됩니다.

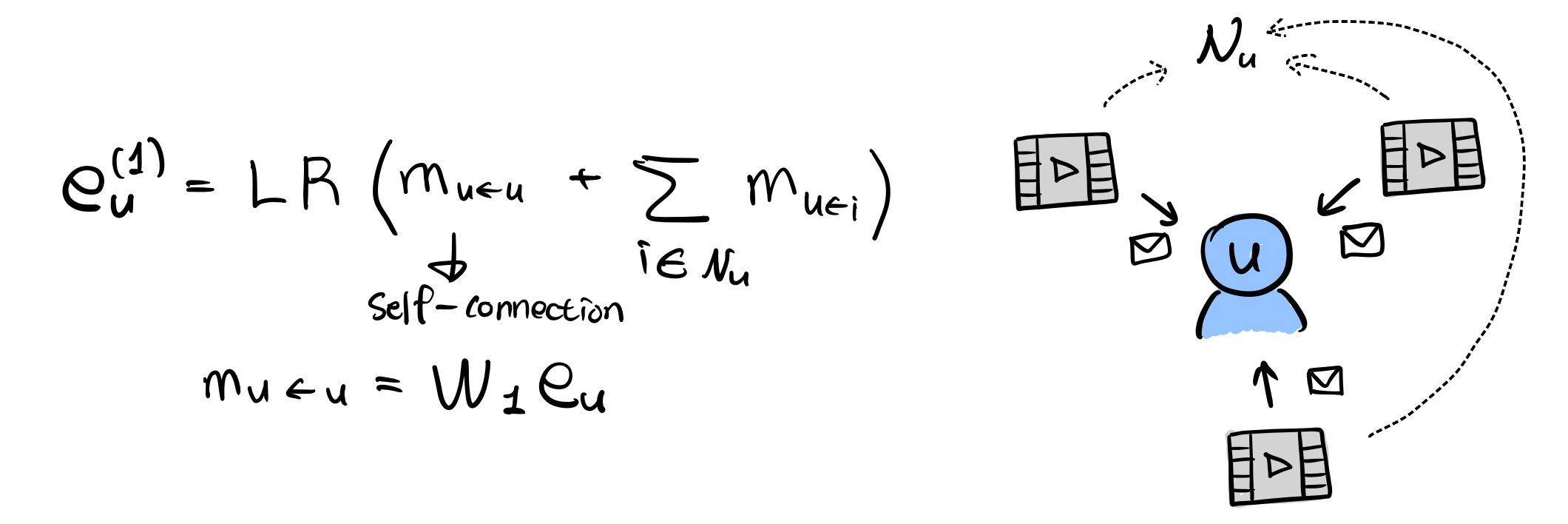
요약하자면 전파 레이어의 장점은 1차 연결 정보(first-order connection information)를 이용하여 유저와 아이템 각각의 표현을 연관짓게 한다는 것입니다!

2. High-order propagation

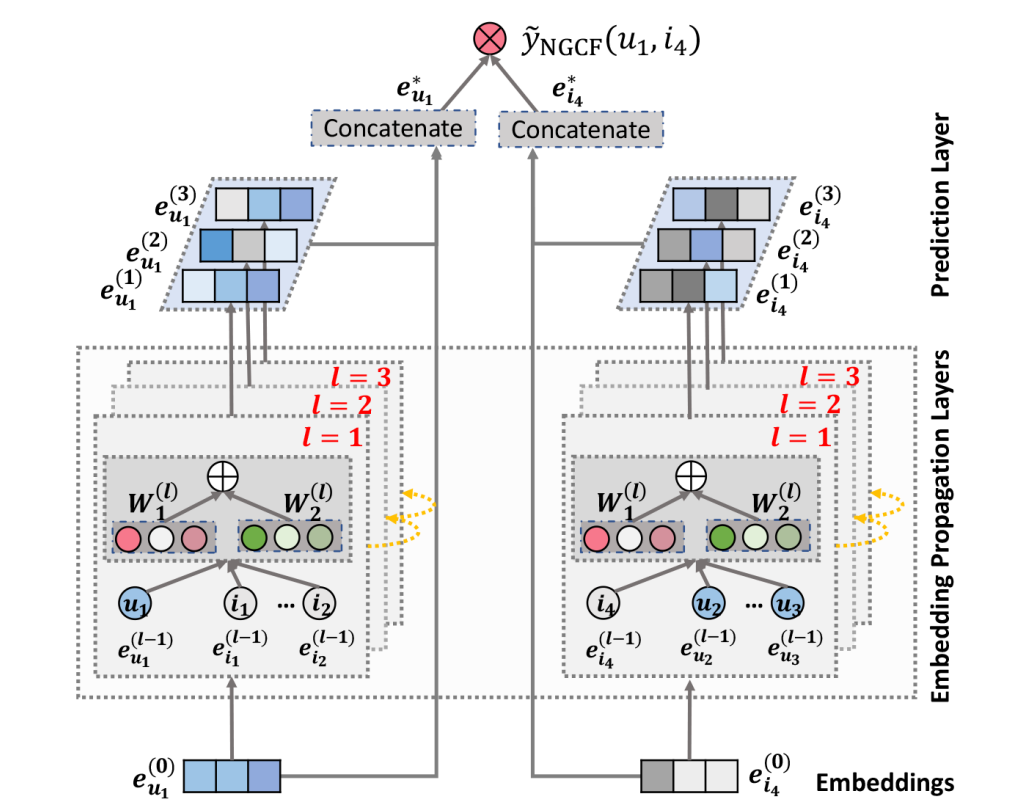Figure2. NGCF 아키텍쳐. 화살표는 정보가 흐른다는 것을 의미한다. 그림 가장 밑에 \(u_1\)과 \(i_4\)가 있다. 각각 여러개의 임베딩 전파 레이어를 거치고 마지막엔 레이어의 아웃풋들이 concat되어, 최종 예측 스코어 계산에 쓰인다.

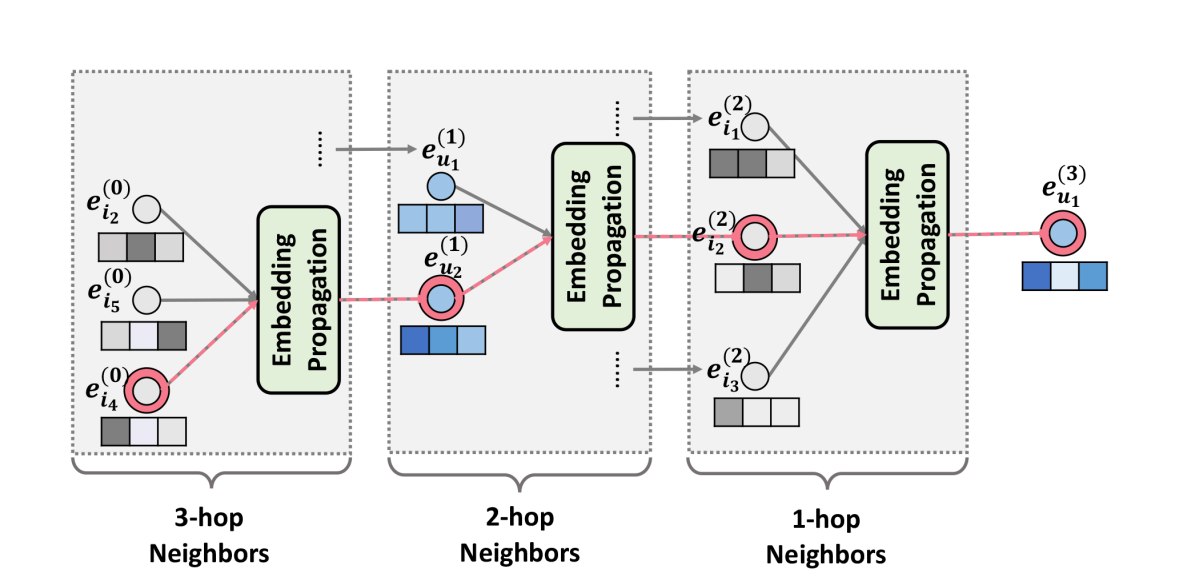Figure3. \(u_1\)에 대한 3차(third-order) 임베딩 전파

1차로 얻은 연결성 모델링을 통해 좀 더 강화된(augmented) 표현을 얻었습니다. 레이어를 더 쌓아 고차원 연결의 정보를 얻을 수 있습니다. 이런 고차원 연결성(high-order connectivity)은 CF 시그널을 인코딩하는데에 매우 중요하겠죠?

\(l\)개의 전파 레이어를 쌓음으로써, 유저(혹은 아이템)은 자신의 \(l\)-hop으로부터 전파된 메시지를 받을 수 있습니다. Figure 2를 통해 볼 수 있는 것처럼, \(l\)번째 스텝에서는 유저 \(u\)의 표현이 재귀적으로 다음과 같이 공식화됩니다:

\[e_u^{(l)} = \text{LeakyReLU}(m_{u \leftarrow u}^{(l)} + \sum_{i \in N_u}m_{u \leftarrow i}^{(l)})\]

그렇다면 \(l\)-hop으로부터 오는 메시지는 어떻게 공식화될까요? 다음과 같습니다. 이런 식으로 재귀적으로 수행되겠죠:

\[m_{u \leftarrow i}^{(l)} = p_{ui}(W_1^{(l)}e_i^{(l-1)} + W_2^{(l)}(e_i^{(l-1)} \odot e_u^{(l-1)}))\] \[m_{u \leftarrow u}^{(l)}=W_1^{(l)} e_u^{(l-1)}\]

\(W_1^{(l)}, W_2^{(l)} \in \mathbb{R}^{d_l \times d_{l-1}}\)은 학습가능한 transformation 행렬이고, \(d_l\)은 변형 후 사이즈입니다. \(e_i^{l-1}\)은 이전 스텝으로부터 생성된 아이템 표현입니다. 이 표현은 \((l-1)\)-hop 이웃으로부터의 메시지를 기억하고 있습니다. Figure 3에서 볼 수 있듯이, \(u_1 \leftarrow i_2 \leftarrow u_2 \leftarrow i_4\)와 같은 collaborative signal이 전파 과정에 의해 학습될 수 있습니다. \(i_4\)로부터의 메시지는 \(e_{u_1}^{(3)}\)에 명시적으로 인코딩됩니다.

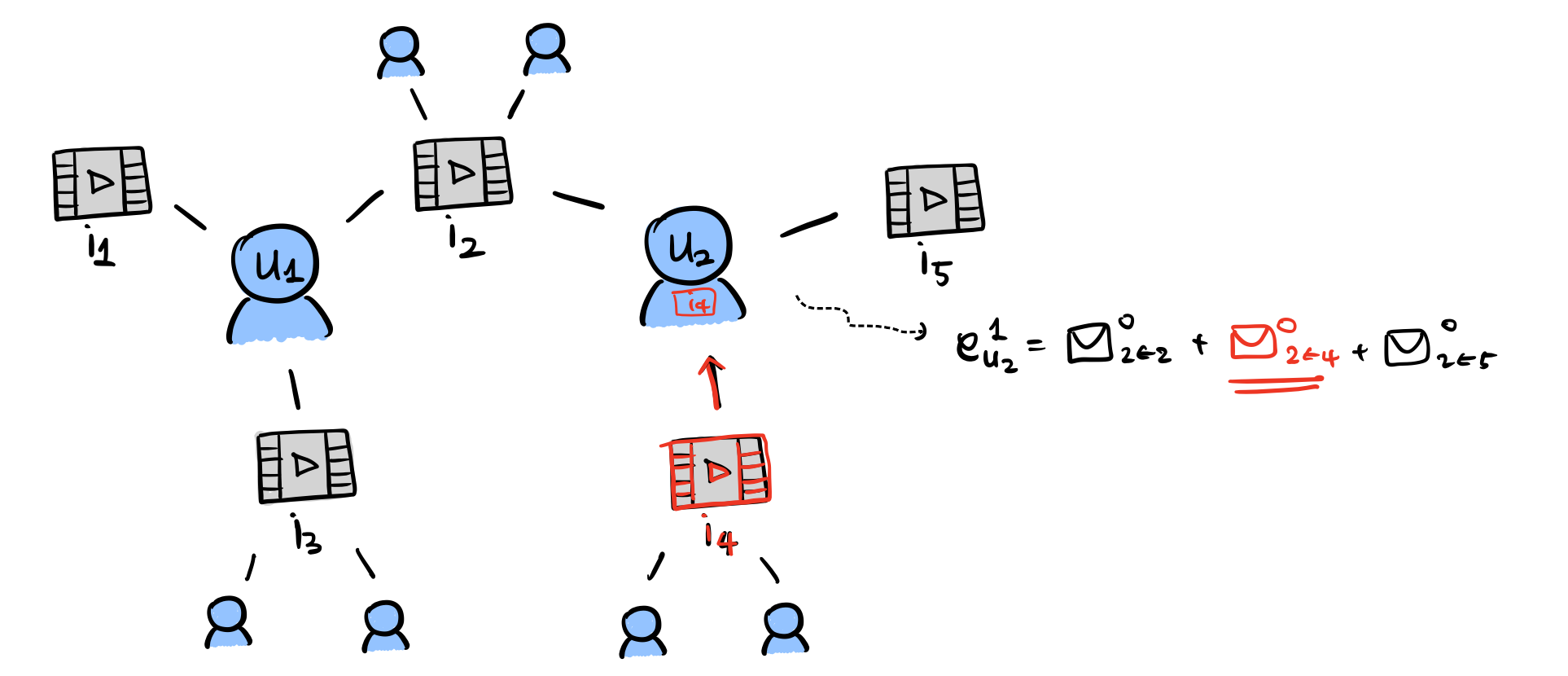
4번 아이템 \(i_4\)에서 1번 유저 \(u_1\)까지의 메시지, \(m_{4 \leftarrow 1}\)가 어떻게 구해지는지 다시 한 번 천천히 살펴봅시다.

위와 같은 그래프(Figure 3과 동일)가 있다고 할 때, 가장 첫 작업(첫 번째 레이어)에서 \(u_2\)는 \(i_4\)로부터 오는 메시지를 받아 업데이트 될 것입니다. 즉, \(e_{u_2}^{(1)}\)은 \(i_4\) 정보를 포함하게 됩니다. 물론 이 단계에서 모든 아이템과 유저 임베딩이 동일하게 업데이트 될 것입니다.

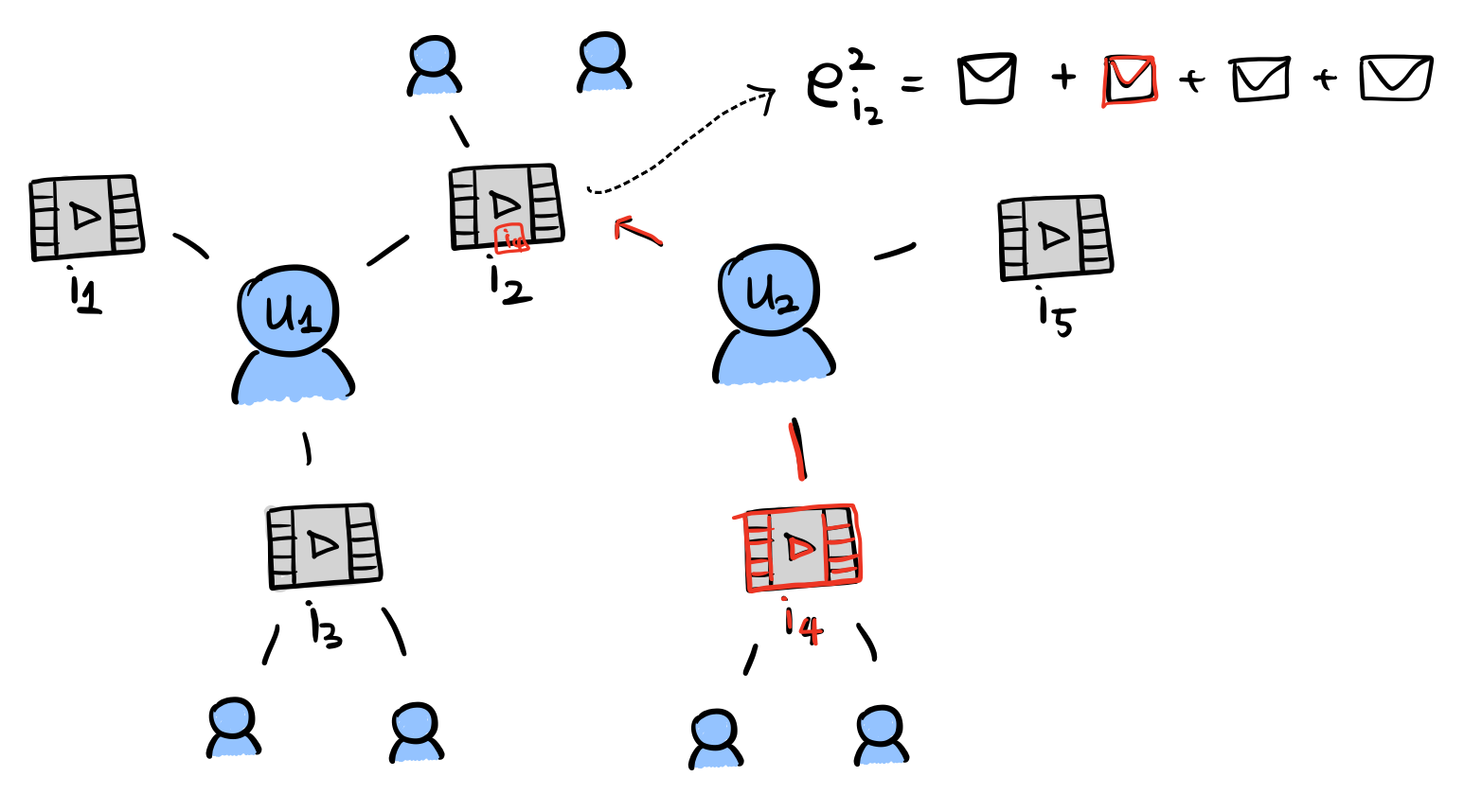
두 번째 작업(레이어)에서는 \(i_2\) 주변 유저들로부터 메시지를 받아 업데이트 될 것입니다. 그런데 이 유저 중 한 명인 \(u_2\)는 이전 레이어에서 \(i_4\)의 정보를 포함하게 됐었죠. 그래서 두 번째 레이어까지 업데이트를 마친 결과, 결과적으로 \(i_4\)의 정보를 포함한 \(u_2\), \(u_2\)의 정보를 포함한 \(i_2\)가 되었습니다.

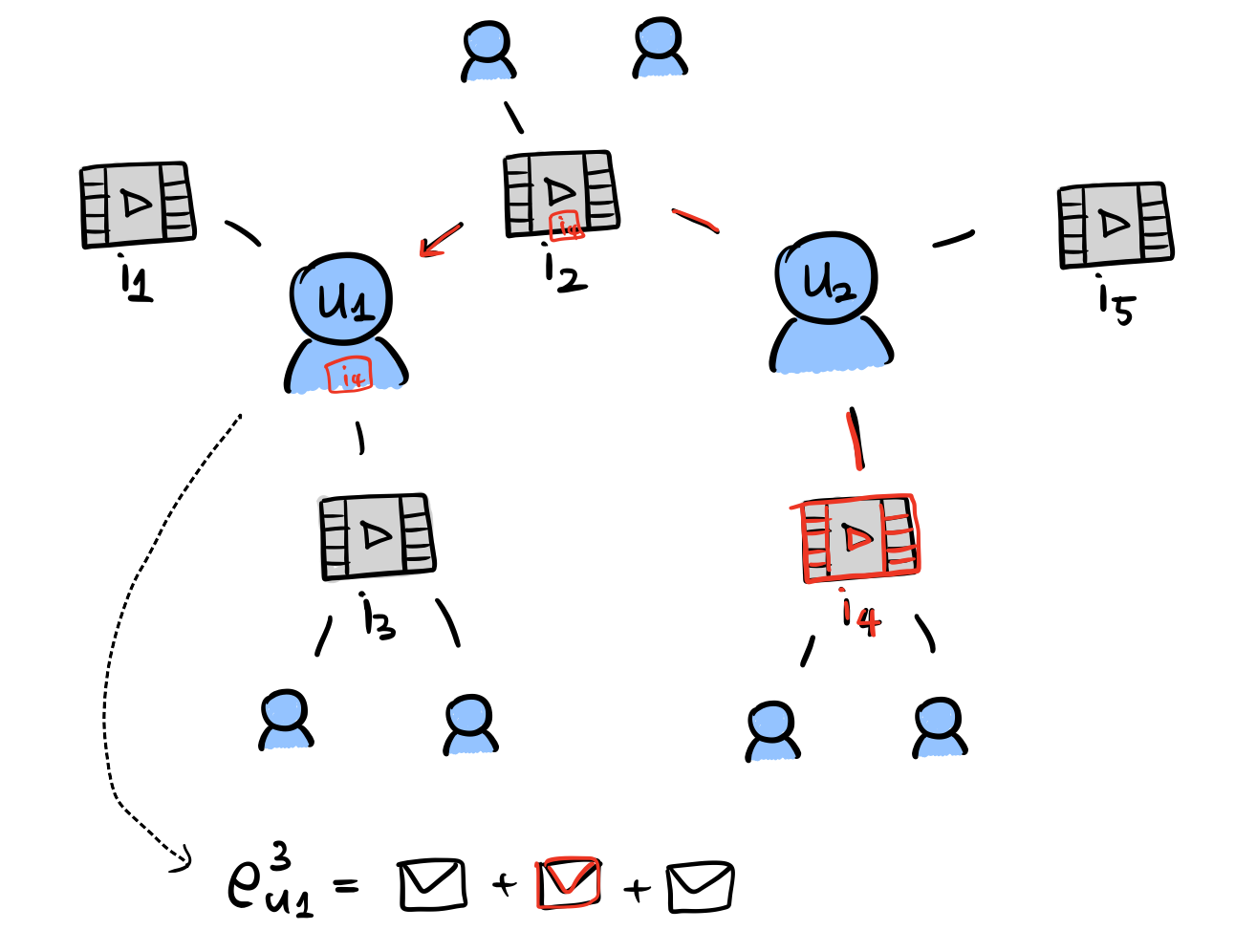
그 다음단계에서 \(u_1\)은 마찬가지로 주변 아이템 \(i_1, i_2, i_3\)로부터 메시지를 맞아 업데이트 되겠죠. 근데 \(i_2\)는 \(i_4\)의 정보까지 포함하고 있었네요. 따라서 이번 레이어에서의 작업을 마치면 \(u_1\)은 \(i_4\)의 정보까지 포함하게 될 것입니다.

즉, 메시지 전파를 전체적으로 3판(?) 수행하면 각 판마다 \(\mathbf{e}^1_{u_1}, \mathbf{e}^2_{u_1}, \mathbf{e}^3_{u_1}\)이 생길텐데, 이 중 \(\mathbf{e}^3_{u_1}\)은 \(\mathbf{e}^0_{i_4}\)를 받아들이게 되는 것이죠.

Propagation Rule in Matrix Form.

임베딩 전파 및 배치 수행을 위해서는, 실제로는 행렬을 이용해 연산을 수행합니다. 레이어 단위로 수행되는 전파는 아래 수식을 따릅니다.

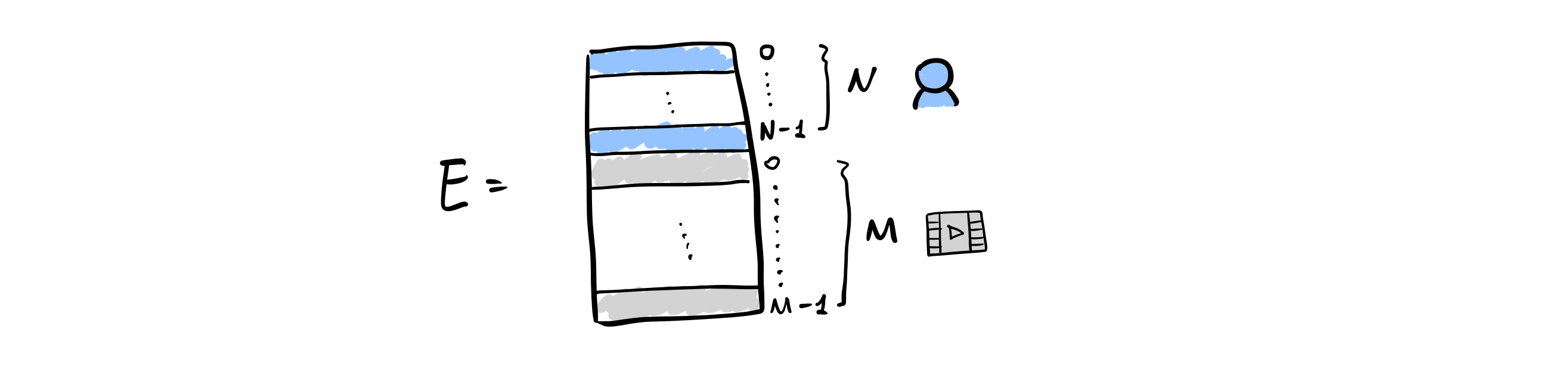
\[E^{(l)} = \text{LeakyReLU}((\mathcal{L}+I)E^{(l-1)}W_1^{(l-1)} + \mathcal{L} E^{(l-1)} \odot E^{(l-1)} W_2 ^{(l)} )\]

\(E\)의 shape는 \(E^{(l)} \in \mathbb{R}^{(N+M) \times d_l }\) 입니다. \(N\)은 유저의 수, \(M\)은 아이템의 수입니다.

\(\mathcal{L}\)은 유저-아이템 그래프에 대한 Laplacian 행렬이며 다음과 같이 정의됩니다:

\[\mathcal{L} = \mathbf{D}^{-\frac{1}{2}}\mathbf{A}\mathbf{D}^{-\frac{1}{2}} \\ \\ \\ \;\; \text{and}\;\; \mathbf{A}=\begin{bmatrix} \mathbf{0} & \mathbf{R} \\ \mathbf{R}^\top & \mathbf{0} \end{bmatrix}\]

\(\mathbf{R} \in R^{N \times M}\)은 유저-아이템 상호작용 행렬이며, \(\mathbf{0}\)는 영행렬입니다. \(\mathbf{A}\)는 인접행렬이며, \(\mathbf{D}\)는 대각 degree 행렬입니다. \(\mathbf{D}\)의 \(t\)-th 대각 요소는 \(D_{tt} = |\mathcal{N}_t|\), 즉 이웃의 수 입니다.

뭔 말인가 싶어서 Laplacian 행렬에 대해 찾아보고 직접 예를 들어 계산해봤습니다.

\(\mathcal{L} = \mathbf{D}^{-\frac{1}{2}}\mathbf{A}\mathbf{D}^{-\frac{1}{2}}\)가 등장한 이유

\(\mathcal{L} = \mathbf{D}^{-\frac{1}{2}}\mathbf{A}\mathbf{D}^{-\frac{1}{2}}\)는 어떤 노드가 주변 노드의 정보를 aggregation할 때 그 message의 decay factor가 들어있는 행렬입니다.

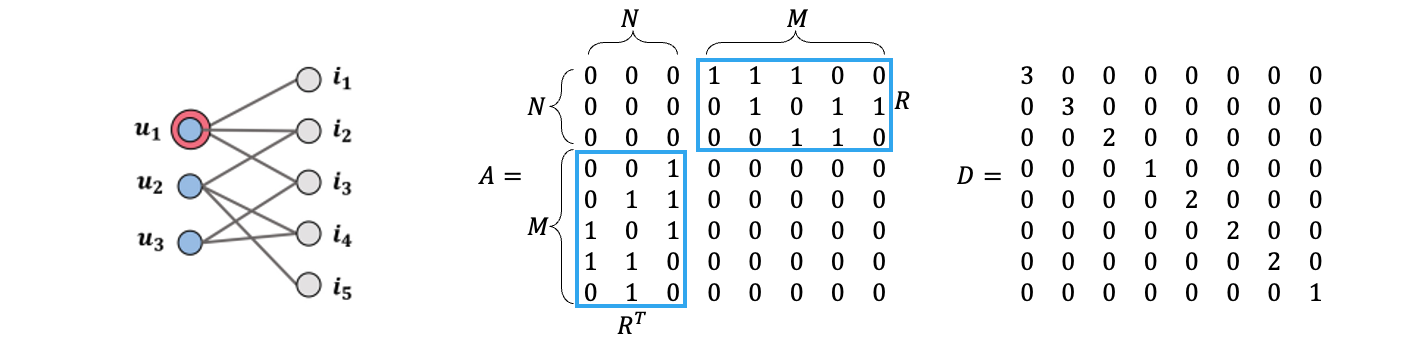
논문에 나오는 그래프를 예로 들어봅시다. 3명의 유저와 5개의 아이템이 있습니다. 본 논문에서 정의한 인접행렬 \(\mathbf{A}\)에는 \(\mathbf{R}\)이라는 인터랙션 행렬이 블록행렬 형태로 들어가 있습니다. 인접행렬에서 1이었던 자리는 유저와 아이템의 인터랙션이 존재했음을 의미합니다.

Laplacian \(\mathcal{L} = \mathbf{D}^{-\frac{1}{2}}\mathbf{A}\mathbf{D}^{-\frac{1}{2}}\) 계산을 해봅시다.

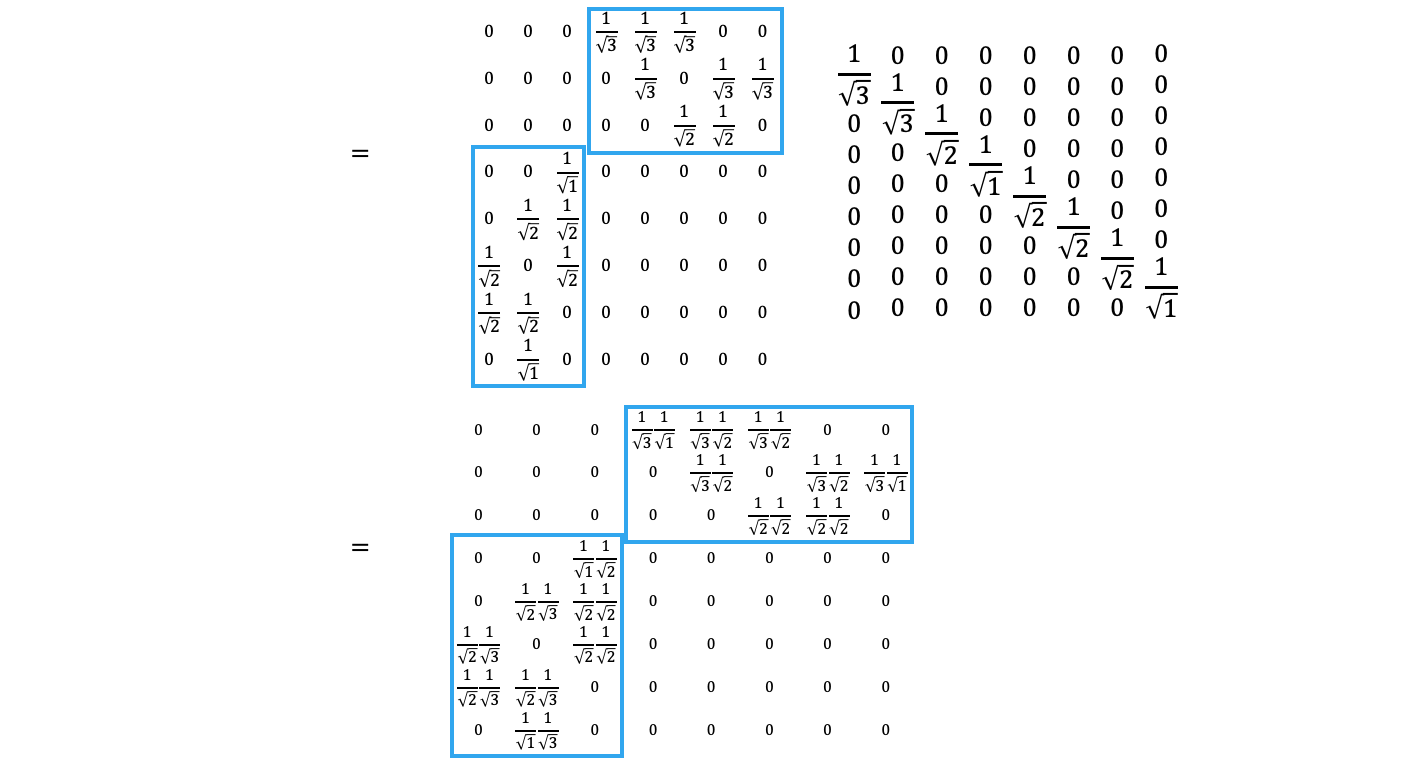
앞뒤로 각 노드의 degree의 \(\frac{1}{\sqrt{\mathcal{\mid N \mid}}}\)을 곱해주니까, 1이 있던 자리에는 유저의 이웃 수와 아이템의 이웃 수를 각각 루트를 씌워 역수를 취한 후 두 수를 곱한 수가 되었습니다.

이 숫자의 의미는 앞 장에서 설명했던 것처럼, 인기가 많은 아이템(다른 유저와 인터랙션이 많은 아이템)으로부터의 메시지의 정보 크기는 그 이웃 수만큼 줄인다는 것입니다.

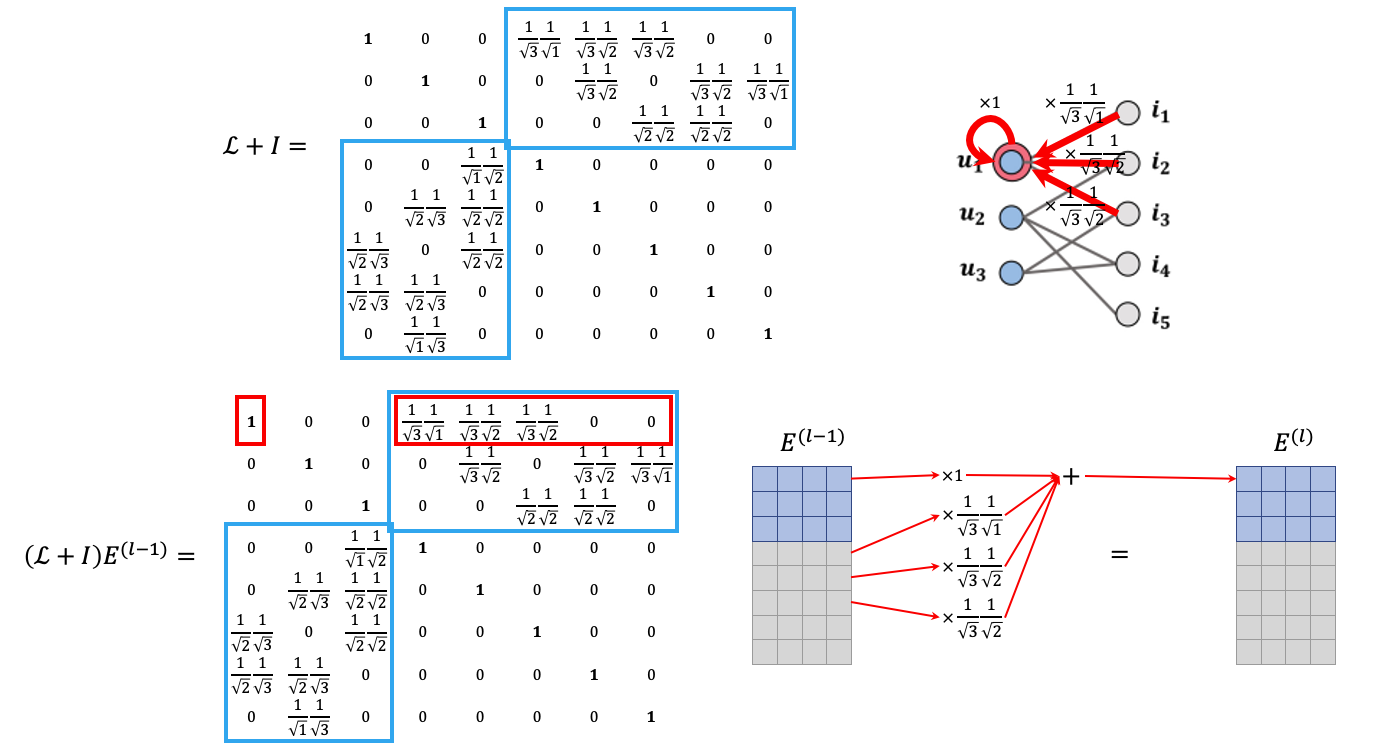
\((\mathcal{L} + I)E\)를 수행하게 되면, 연결된 주변 노드로부터 decay factor가 곱해진 정보를 받아들여 더해지게 됩니다.

이제 \(E^{(l)} = \text{LeakyReLU}((\mathcal{L}+I)E^{(l-1)}W_1^{(l-1)} + \mathcal{L} E^{(l-1)} \odot E^{(l-1)} W_2 ^{(l)} )\) 이 수식이 좀 보이시나요? \(\mathcal{L}_{ui} = 1 / \sqrt{|\mathcal{N}_u||\mathcal{N}_i|} = p_{ui}\)가 됩니다. 이 수는 message construction에서 봤던 그 계수와 동일합니다.

행렬 계산 형태로 propagation을 수행함으로써, 우리는 모든 유저와 아이템에 대한 표현을 동시에 효과적으로, 한 번에 업데이트할 수 있습니다. Graph convolutional network(2018. DeepInf: Social Influence Prediction with Deep Learning.)에서는 보통 노드 샘플링 과정이 있는데, 이렇게 행렬 계산을 함으로써 이 과정도 없어집니다.

3. Model Prediction

\(L\)번의 propagating을 거치고 난 후 유저 \(u\)에 대해 여러 개의 representation, 즉 \({ \mathbf{e}_u^{(1)}, \cdots, \mathbf{e}_u^{(L)} }\)을 얻게 된다. 각 레이어마다의 representation들은 다른 커넥션들을 거쳐 패싱되어왔기 때문에 유저의 선호도에 각기 다른 측면을 갖고 있다. 각각 공헌한다. 그래서 이들은 concat한다. 아이템도 똑같이 \(u\)와 \(i\)에 대한 final embedding은 다음과 같다.

\[\mathbf{e}_u^* = \mathbf{e}_u^{(0)} \parallel \cdots \parallel \mathbf{e}_u^{(L)}, \mathbf{e}_i^* = \mathbf{e}_i^{(0)} \parallel \cdots \parallel \mathbf{e}_i^{(L)}\]

최종적으로, 유저 \(u\)의 아이템 \(i\)에 대한 선호도를 계산하기 위해 내적한다.

\[\hat{y}_{\text{NGCF}} (u, i) = {\mathbf{e}_u^*}^\top \mathbf{e}_i^*\]

4. Optimization (BPR)

pairwise BPR loss (2009. BPR: Bayesian Personalized Ranking from Implicit Feedback.)를 최적화했다. 이는 추천시스템에서 광범위하게 쓰인다. 이는 관측된, 그리고 관측 안 된(observed and unobserved) 인터랙션 사이의 상대적인 순서를 고려합니다. BPR은 ‘observed 아이템은 unobserved 아이템보다 유저의 선호도에 더욱 크게 반영되어야 하고, 더 높은 예측 값을 가져야한다’를 가정합니다. 목적 함수는 다음과 같습니다:

\[\text{Loss} = \sum_{(u, i, j) \in \mathcal{O}} -\ln \sigma (\hat{y}_{ui} - \hat{y}_{uj}) + \lambda \parallel \Theta \parallel_2^2\]

\(\mathcal{O} = \left\{ (u, i, j) | (u, i) \in \mathcal{R}^+ , (u, j) \in \mathcal{R}^- \right\}\)은 pairwise 형태의 학습 데이터입니다. \(\mathcal{R}^+\)는 observed interactions을 ,\(\mathcal{R}^-\)는 unobserved interactions를 나타냅니다.

\(\sigma (\cdot)\)은 sigmoid function이구요. \(\Theta = \left\{ \mathbf{E}, \left\{ \mathbf{W}_1^{(l)}, \mathbf{W}_2^{(l)} \right\}_{l=1}^{L} \right\}\)는 모든 학습 가능한 파라미터들을 의미합니다. 그리고 \(\lambda\)는 파라미터의 오버피팅을 막기 위한 \(L_2\) regularization 강도를 조절합니다.

특히, \((u, i, j) \in \mathcal{O}\)는 랜덤하게 샘플링하는데, 이 때 \(L\)번의 propagation을 통해 representation \(\left[ \mathbf{e}^{(0)}, \cdots, \mathbf{e}^{(L)} \right]\)을 먼저 구하고, 그 다음에 손실 함수의 gradient를 사용하여 파라미터를 업데이트합니다.