nDCG의 기본 수식은 다음과 같습니다 :

\[NDCG@K = Z_K \sum_{i=1}^{K} \frac{2^{rel_i}-1}{\log_2(i+1)}\]

\(Z_K\)는 제일 좋은 성능일 때를 1로 만들기 위한 normalizer입니다. 보통은 1로 놓습니다. \(rel_i\)는 \(i\)번째 아이템의 graded relavance입니다. implicit data이기 때문에 \(rel_i\)는 1 또는 0이며, 1일 때는 아이템이 test set에 존재할 때이고, 0일 때는 그렇지 않을 때입니다.

예시

예를 들어 K=5라고 해보겠습니다.

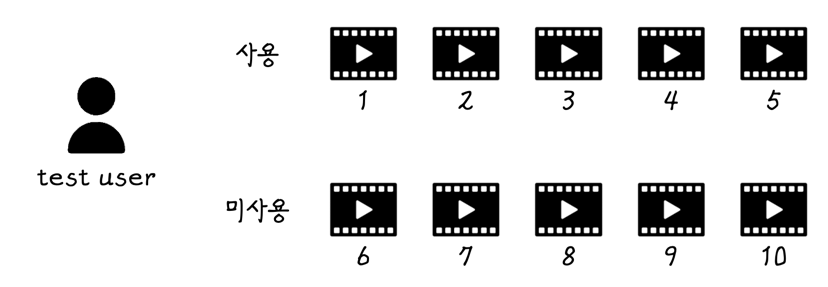
다음과 같이 t라는 유저가 있고, 이 유저는 1~5까지 5개의 아이템을 사용(클릭)했고 6~10 아이템은 사용하지 않았다고 해봅시다.

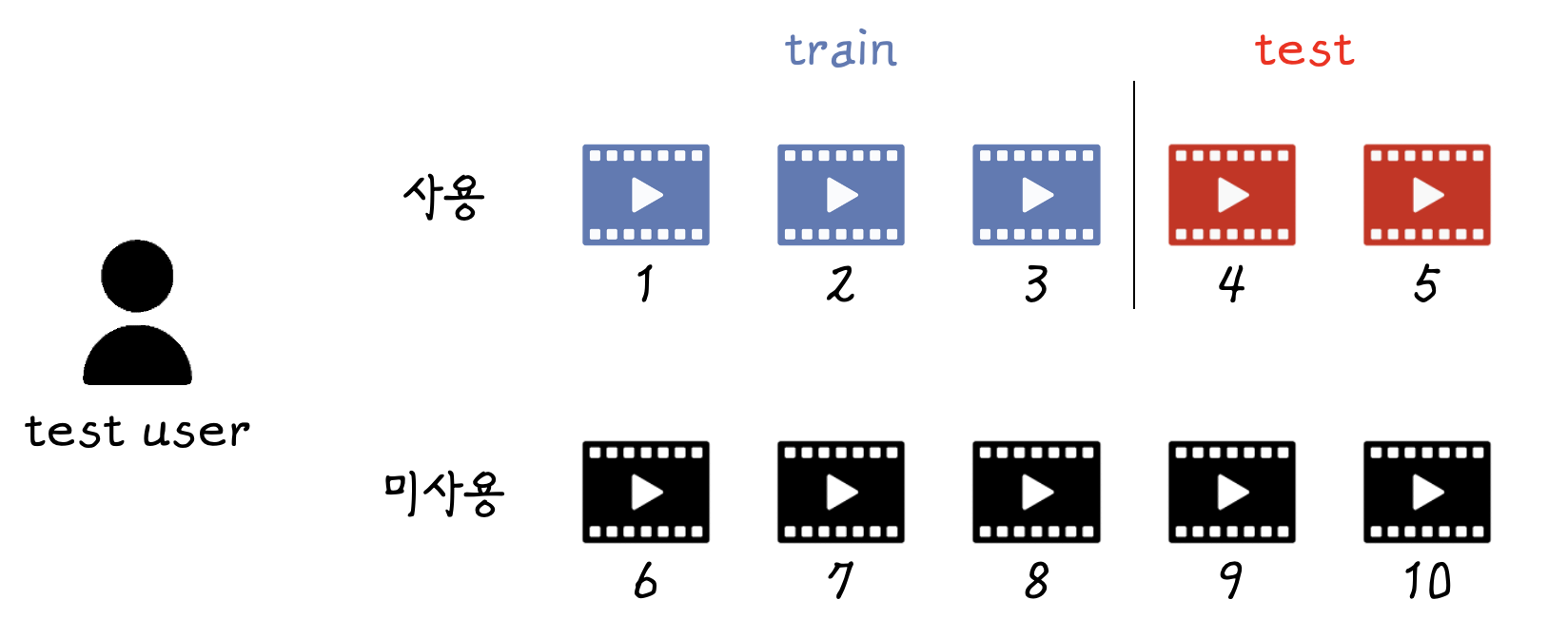
사용한 아이템을 train과 test로 나누게 될 것입니다. 그리고 train으로 학습이 진행될 것입니다. 이제 테스트 시간이 왔다고 해봅시다.

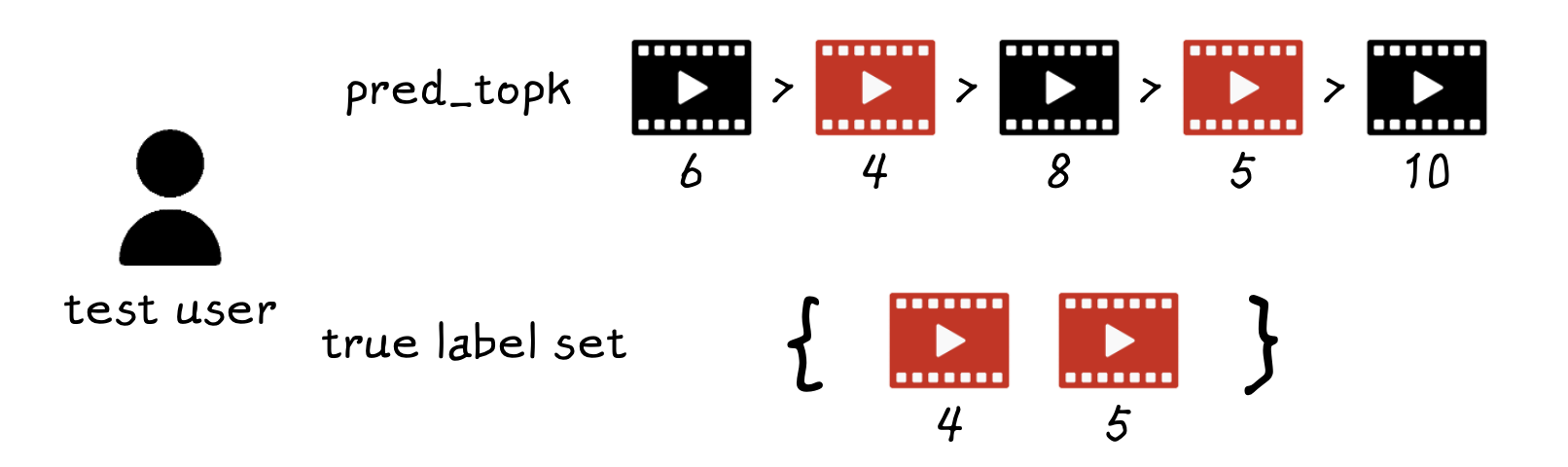
모델이 다음 클릭으로 예측한 결과가 6, 4, 8, 5, 10 순으로 높은 스코어가 나왔다고 해봅시다. 테스트 유저가 실제로 클릭한 test셋인 아이템은 4, 5입니다. 모델이 4, 5를 높은 순위로 예측했다면 좋은 모델이라고 할 수 있습니다. 이 true label set, 즉 test set인 4, 5 아이템 간의 시간 순서 등은 사용되지 않습니다.

idcg를 구해봅시다. idcg는 모델 예측이 true label set으로 1위부터 쭉 나열된 경우, 말그대로 ideal한 상황에서 DCG를 계산한 값입니다. 위 수식에 따르면 :

\[\begin{align*}\text{idcg(ideal dcg)} &= \sum_{i=1}^{k} \frac{2^{r_i}-1}{\log_2(i+1)}\\ &=\frac{1}{\log_2{(1+1)}}+\frac{1}{\log_2{(2+1)}}+\frac{0}{\log_2{(3+1)}}+\frac{0}{\log_2{(4+1)}}+\frac{0}{\log_2{(5+1)}}\\ &=1.6309 \end{align*}\]

4, 5 아이템이 1, 2등인 상황에서 구한 값입니다.

이제 dcg를 구해봅시다. dcg는 \(k=5\)까지 계산한 값입니다:

\[\begin{align*}\text{dcg} &= \sum_{i=1}^{k} \frac{2^{r_i}-1}{\log_2(i+1)}\\ &=\frac{0}{\log_2{(1+1)}}+\frac{1}{\log_2{(2+1)}}+\frac{0}{\log_2{(3+1)}}+\frac{1}{\log_2{(4+1)}}+\frac{0}{\log_2{(5+1)}}\\ &=1.0616 \end{align*}\]

\(ndcg=\frac{dcg}{idcg}\)로 계산합니다.

그러므로 \(\text{nDCG@5}=\frac{dcg}{idcg}=\frac{1.0616}{1.6309}=0.6509\)

논문 TriRank: Review-aware Explainable Recommendation by Modeling Aspects의 일부를 참고했습니다.