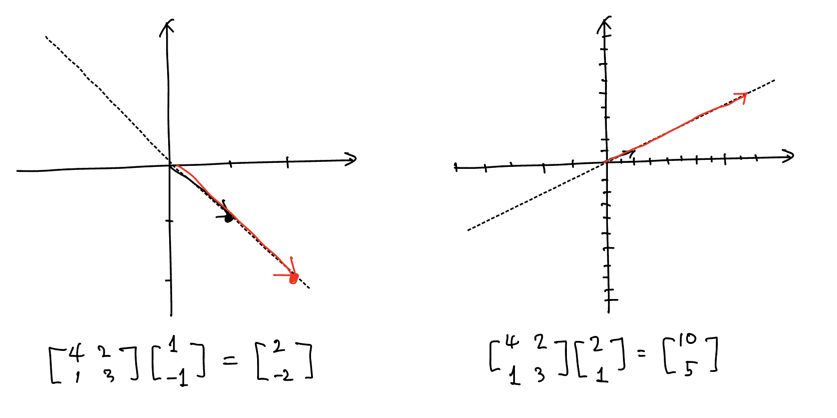행렬의 특성과 선형 사상(linear mapping)을 새로운 관점으로 살펴보자!
선형 사상(linear mapping)이란?
간단히 말해서, 두 벡터를 더한 후 매핑한 결과랑, 각각 매핑하고 더한 결과가 같으면 이 매핑은 linear mapping이다.
내가 이해하기론 ‘선형 사상 = 행렬 곱’ 이다.
모든 선형 사상은 ordered basis에 대해 고유한 변환 행렬(transformation matrix)를 갖는다. linear mapping과 이에 연관된 변환 행렬들은 “고유(eigen)” 분석을 하는 거라고 볼 수 있다. 앞으로 살펴보겠지만, 고유벡터(eigenvectors)라고 하는 특별한 벡터들이 선형 사상에 의해 어떻게 변형되는가를 고유값(eigenvalue)을 통해 알 수 있다.
Definition 4.6. \(A \in \mathbb{R}^{n \times n}\)를 정방행렬이라고 하자. \(A\)가 \(Ax=\lambda x\)를 만족한다면, \(\lambda \in \mathbb{R}\)를 \(A\)의 고유값(eigenvalue)라고 부르고, \(x \in \mathbb{R}^n \backslash \left\{ 0 \right\}\)은 이에 상응하는 고유벡터(eigenvector)라고 부른다.
이를 고유값 방정식(eigenvalue equation)이라고 한다.
Definition 4.7 (Collinearity and Codirection). 같은 방향을 가리키는 두 벡터를 codirected라고 부른다. 같은 방향을 가리키거나 반대 방향을 가리키는 경우엔 collinear라고 한다.
비고. 만약 \(x\)가 \(A\)의 고유벡터이고 \(\lambda\)가 고유값이라면, 어떠한 \(c \in \mathbb{R} \backslash \left\{ 0 \right\}\)에 대해서 \(cx\)는 A의 고유벡터이다. 왜냐하면 \(A(cx) = cAx = c \lambda x = c \lambda x = \lambda (cx)\), 즉 \(A(cx) = \lambda (cx)\) (고유값 방정식 만족!)이기 때문이다. 그러므로, x와 collinear 관계에 있는 모든 벡터들 또한 A의 고유벡터이다.
기하학적으로 0이 아닌 고유값에 대한 고유벡터는 선형 사상에 의해 고유값만큼 늘어난다(stretched). 그리고 고유벡터는 선형 사상 \(\phi\)에 의해 방향이 변하지 않는 벡터이다.
행렬 \(A\)와 \(A\)의 전치행렬 \(A^\top\)는 같은 고유값을 갖는다. 하지만 반드시 같은 고유벡터를 갖지는 않는다!
고유값, 고유벡터 계산를 계산해보자. 들어가기에 앞서, kernel(=null space)에 대한 정의 리마인드 해보자.
Example 4.5 고유값, 고유벡터, 고유공간(Eigenspace) 계산하기
아래의 2 X 2 행렬 \(A\)에 대해 고유값과 고유 벡터를 찾아보자.
\[A = \begin{bmatrix} 4 & 2 \\ 1 & 3 \end{bmatrix}\]Step 1: 특성방정식(Characteristic Polynomial)
고유값과 고유벡터의 정의에 따라 \(Ax=\lambda x\), 즉, \((A-\lambda I)x=0\)를 만족하는 벡터 \(x \ne 0\)가 존재할 것이다.
다시 \(Ax=\lambda x\)를 자세히 보면, \((A - \lambda I)x=0\)을 만족하는 \(0\)벡터가 아닌 \(x\)가 고유벡터이다.
고유벡터를 구하고 싶은데, 잠시 \((A-\lambda I)^{-1}\)이 존재하는지 아닌지 보자. \((A-\lambda x)^{-1}\)가 존재한다면, \((A - \lambda I)x=0\)의 양변에 \((A-\lambda x)^{-1}\)를 곱하면 \(x = \mathbf{0}\)이 될 수밖에 없다.
고로 고유값, 고유벡터의 정의에 의해 \((A-\lambda x)^{-1}\)는 존재하지 말아야 한다. 이 말은 \((A-\lambda x)\)는 not invertible하다는 것과 동일한 말이고, \(\text{det}(A-\lambda I) = 0\)이라는 것이다.
즉, \(\text{det}(A-\lambda I) = 0\) 식의 \(\lambda\)를 구하면 그 값이 고유값이다! 와우.
행렬 \(A\)의 특성 다항식은 \(p_{A}(\lambda) := det(A - \lambda I)\)로 정의된다. \(\lambda\)는 스칼라 값이다. 특성다항식의 근은 행렬 \(A\)의 고유값이라는 것이다.
Step 2: 고유값
\[\begin{align} p_A(A) &= \text{det}(A - \lambda I) \\ &= \text{det}(\begin{bmatrix} 4 & 2 \\ 1 & 3 \end{bmatrix} - \begin{bmatrix} \lambda & 0 \\ 0 & \lambda \end{bmatrix}) \\ &= \begin{vmatrix} 4-\lambda & 2 \\ 1 & 3 - \lambda \end{vmatrix} \\ &= (4 - \lambda)(3 - \lambda) - 2 \cdot 1 \\ &= \lambda^2 - 7\lambda + 10 \\ &= (2-\lambda)(5-\lambda) \end{align}\]근 \(\lambda_1 = 2\)와 \(\lambda_2 = 5\)를 얻었다.
Step 3: 고유벡터와 고유값
고유값에 상응하는 고유벡터를 다음 식으로 얻을 수 있다:
\[\begin{bmatrix} 4 - \lambda & 2 \\ 1 & 3 - \lambda \end{bmatrix}x = \mathbf{0}\]\(\lambda = 5\)에 대하여 아래 식이 된다.
\[\begin{bmatrix} 4 - 5 & 2 \\ 1 & 3 - 5 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} -1 & 2 \\ 1 & -2 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \mathbf{0}\]이를 만족하는 \(x\)는 \(x_1 = 2x_2\)을 만족하는 \(x = \begin{bmatrix} x_1 \\ x_2 \end{bmatrix}\)라면, 예를 들면 \(\begin{bmatrix} 2 \\ 1 \end{bmatrix}\)같은 벡터가 모두 해가 된다.
\(\lambda = 2\)에 대해서도 똑같이 풀면, \(x_1 = -x_2\)을 만족하는 \(x = \begin{bmatrix} x_1 \\ x_2 \end{bmatrix}\)라면, 예를 들면 \(\begin{bmatrix} 1 \\ -1 \end{bmatrix}\)같은 벡터가 모두 해가 된다.