추천시스템과 Matrix Decompositions — 3. 고유값과 고유벡터, Cholesky Decomposition

이번엔 내용이 좀 많고 어려웠습니다..! Matrix decomposition의 원리를 다 이해해보려고 며칠동안 독기품고 정리했습니다..!! 말투를 반말로 바꾸겠습니다 😄

좌표를 잃지 않기 위해 4단원 ‘Matrix Decompositions의 목차를 다시 한 번 정리하고 오늘 다룰 부분을 알아보자.

4.1 Determinant and Trace

4.2 Eigenvalues and Eigenvectors ← 여기 끝부분

4.3 Cholesky Decomposition ← 여기

4.4 Eigendecomposition and Diagonalization ← 여기

4.5 Singular Value Decomposition

이번 글에서 다룰 내용은 4.2의 끝부분, 4.3, 4.4 단원이다.

뒤에도 더 있지만, SVD까지 정리하는 것을 목표로 하고 있다!

Eigenvector 이야기가 아직 끝나지 않았다!

Example 4.9 (Google’s PageRank - Webpages as Eigenvectors) 구글은 행렬 \(A\)의 고유값 중 최대값에 대응되는 고유벡터를 이용하여 검색 시 페이지에 대한 랭크를 결정한다. 이러한 ‘PageRank’라고 불리는 알고리즘은 1996년 스탠포드 대학교의 래리 페이지(Larry Page)와 세르게이 브린(Sergey Brin)에 의해 탄생했다. 어느 웹페이지의 중요도는 해당 웹페이지를 링크한 페이지의 중요도에 의해 계산될 수 있다. 개발자들은 모든 웹사이트들을 하나의 거대한 directed graph로 만든 후, 각 페이지가 어디에 링크되는지 보았다. PageRank는 웹사이트 \(a_i\)의 가중치(중요도) \(x_i \geqslant 0\)로 \(a_i\)를 가리키는 페이지의 수를 사용한다. 추가적으로, \(a_i\)를 가리키는 웹사이트의 중요도도 고려한다. 어느 유저의 탐색은 이 그래프의 전이 행렬(transition matrix) \(A\)로 나타낼 수 있을 것이다. 그럼 이 행렬은 누군가가 얼마의 확률로 어느 페이지에 도달할지 알려준다. 어느 웹사이트의 초기 중요도 벡터를 \(x\)라고 해보자. \(x\), \(Ax\), \(A^2x\), \(\cdots\) 가 \(x^*\)라는 벡터로 수렴한다. \(A\)의 특성이 그렇다. 이 벡터 \(x^*\)를 PageRank라고 부르며, \(Ax^*=x^*\)를 만족한다. 즉, 어느 웹사이트의 중요도 벡터는 행렬 \(A\)의 고유값 1에 상응하는 고유벡터인 셈이다. \(x^*\)를 정규화하면(\(||x^* || = 1\)), 각 요소는 확률로 해석될 수 있다. 상세한 사항은 원논문 Page et al., 1999에서 찾아볼 수 있다.

Graphical Intuition in Two Dimensions

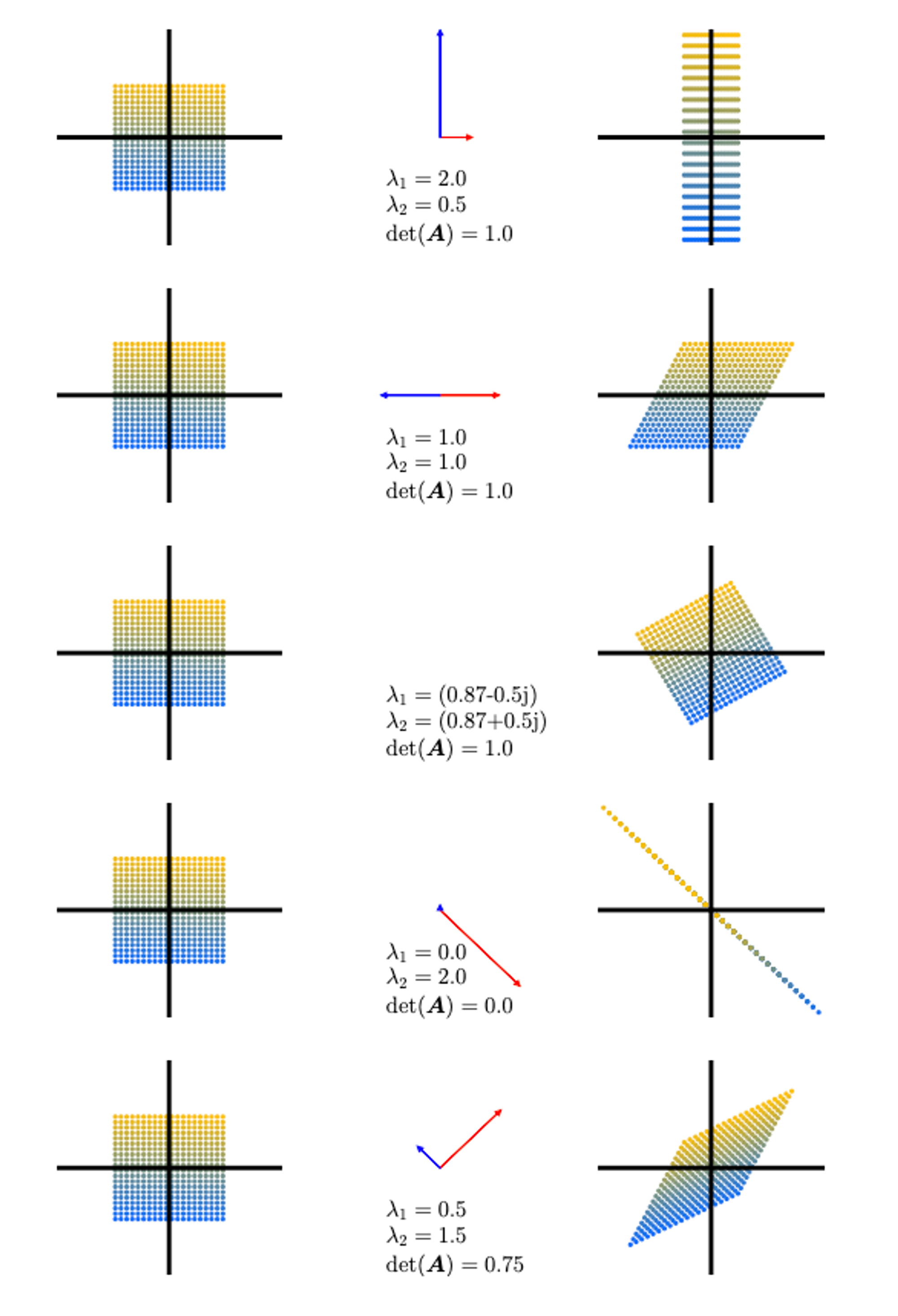
determinants, eigenvectors, 그리고 eigenvalues에 대해 직관적인 이해로 들어가보자. Figure 4.4는 행렬 \(\mathbf{A}_1\), …, \(\mathbf{A}_5\)와 이들에 의한 점들의 변형을 보여주고 있다.

• \(\mathbf{A}_1 = \begin{bmatrix} \frac{1}{2} & 1 \\ 0 & 2 \end{bmatrix}\). 두 고유벡터들의 방향이 2차원 canonical basis 벡터들과 나란한 상황이다. 수직축 방향으로 2만큼 늘어나고(고유값 \(\lambda_1=2\)), 수평축 방향으로 \(\frac{1}{2}\)만큼 압축된다. 넓이는 보존된다.
• \(\mathbf{A}_2 = \begin{bmatrix} 1 & \frac{1}{2} \\ 0 & 1 \end{bmatrix}\)은 전단 매핑(sheering mapping)인데, 즉, y축의 양의 방향에 있다면 오른쪽으로, 음의 방향에 있다면 왼쪽으로 전단한다. 이 매핑도 넓이를 보존한다. 고유값은 두 값이 동일한 \(\lambda_1=1=\lambda_2\)이며, 고유 벡터들은 collinear이다. 즉, 그림처럼 수평 축 방향으로만 늘어나거나 줄어든다.
• \(\mathbf{A}_3 = \begin{bmatrix} \cos{\frac{\pi}{6}} & -\sin{\frac{\pi}{6}} \\ \sin{\frac{\pi}{6}} & \cos{\frac{\pi}{6}} \end{bmatrix}=\frac{1}{2}\begin{bmatrix} \sqrt{3} & --1 \\ 1 & \sqrt{3} \end{bmatrix}\)은 점들을 \(\frac{\pi}{6}\), 즉 30도만큼 반시계 방향으로 회전시키다. 그리고 허수의 고유값을 갖는다.
• \(\mathbf{A}_4 = \begin{bmatrix} 1 & -1 \\ -1 & 1 \end{bmatrix}\)은 표준 기저에서의 2차원 도메인을 1차원으로 줄이는 매핑이다. 한 고유값이 0이기 때문에, 이에 해당하는 파란색 고유벡터 방향의 점들은 넓이가 0이 된다. 반면 이와 수직인 빨간색 고유벡터 방향으로는 고유값인 \(\lambda_2=2\)만큼 늘어난다.
• \(\mathbf{A}_5 = \begin{bmatrix} 1 & \frac{1}{2} \\ \frac{1}{2} & 1 \end{bmatrix}\)는 전단도 하고 늘리기도 하는 매핑이다. 이 행렬의 determinant는 \(|\det(\mathbf{A}_5)|=\frac{3}{4}\)이기 때문에, 넓이를 75%로 만든다. 빨간 고유벡터 방향의 넓이는 \(\lambda_2=1.5\)에 의해 늘어나고, 파란 고유벡터 방향의 넓이는 \(\lambda_1=0.5\)에 의해 줄어든다.

---

Theorem 4.12. 서로 다른 고유값 \(\lambda_1, ..., \lambda_n\)을 갖는 행렬 \(\mathbf{A}\in \mathbb{R}^{n\times n}\)의 고유벡터 \(x_1, ..., x_n\)는 선형 독립이다.

위 정리는 n개의 서로 다른 고유값을 갖는 행렬의 고유 벡터들은 \(\mathbb{R}^n\)의 기저를 형성한다는 것이 된다.

Definition 4.14. 만약 정방행렬 \(\mathbf{A} \in \mathbb{R}^{n \times n}\)이 \(n\)보다 적은 선형 독립의 고유 벡터를 갖는다면 \(defective\)이다.

\(non-defective\) 행렬 \(\mathbf{A} \in \mathbb{R}^{n \times n}\)이 필수적으로 \(n\)개의 서로 다른 고유값을 필요로 하는 것은 아니다. 하지만, 고유 벡터들이 \(\mathbb{R}^n\)의 기저를 형성해야한다.

---

4.3 Cholesky Decomposition

머신러닝에서 우리가 자주 마주하는 특별한 유형의 행렬을 분해하는데는 다양한 방법들이 있다. 양의 실수에서 \(9\)가 \(3\cdot 3\)으로 분해되는걸 생각해보자. 행렬에 대해서 비슷하게 하려면 좀 조심해야한다. symmetric, positive definite matrices에 대해서는, Cholesky 분해가 유용하다!

Theorem 4.18 (Cholesky Decomposition). Symmetric, positive definite 행렬 \(\mathbf{A}\)는 \(\mathbf{A}=\mathbf{L}\mathbf{L}^{\top}\)로 분해될 수 있다. \(\mathbf{L}\)은 양의 대각 요소를 가진 lower triangular 행렬이다.

\[\begin{bmatrix}a_{11} & \cdots & a_{1n} \\\vdots & \ddots & \vdots \\a_{n1} & \cdots & a_{nn}\end{bmatrix}=\begin{bmatrix}l_{11} & \cdots & 0 \\\vdots & \ddots & \vdots \\l_{n1} & \cdots & l_{nn}\end{bmatrix}\begin{bmatrix}l_{11} & \cdots & l_{1n} \\\vdots & \ddots & \vdots \\0 & \cdots & l_{nn}\end{bmatrix}\]

이 때의 \(\mathbf{L}\)을 \(\mathbf{A}\)의 Cholesky factor라고 부르며, \(\mathbf{L}\)은 유일하다.

Symmetric positive definite 행렬은 3단원에 나오는데, 잠시 살펴보자.

Definition 3.4 (Symmetric, Positive Definite Matrix)

\[\forall x \in V \setminus \left\{ \mathbf{0}\right\} : x^{\top}\mathbf{A} x > 0\]

위 식을 만족하는 대칭 행렬 \(\mathbf{A} \in \mathbb{R}^{n \times n}\)을 symmetric, positive definite, 또는 그냥 positive definite이라고 부른다.

예를 들어 \(\mathbf{A} = \begin{bmatrix} 9 & 6 \\ 6 & 5 \end{bmatrix}\)의 경우, \(\begin{bmatrix} x_1 & x_2 \end{bmatrix} \begin{bmatrix} 9 & 6 \\ 6 & 5 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = (3x_1 + 2x_2)^2 + x_2^2 > 0\)이기 때문에 symmetric, positive definite이다.

이제 symmetric positive definite 행렬에 대해 Cholesky 분해하는 예제를 보자.

Example 4.10 (Cholesky Factorization) Symmetric, positive definite 행렬 \(\mathbf{A} \in \mathbb{R}^{3 \times 3}\)이 있다고 하자. Cholesky 분해 \(\mathbf{A}=\mathbf{L}\mathbf{L}^\top\)을 해보자.

\[\mathbf{A} = \begin{bmatrix}a_{11} & a_{21} & a_{31} \\ a_{21} & a_{22} & a_{32} \\a_{31} & a_{32} & a_{33}\end{bmatrix}=\mathbf{L}\mathbf{L}^{\top}=\begin{bmatrix}l_{11} & 0 & 0 \\ l_{21} & l_{22} & 0 \\l_{31} & l_{32} & l_{33}\end{bmatrix} \begin{bmatrix}l_{11} & l_{21} & l_{31} \\ 0 & l_{22} & l_{32} \\0 & 0 & l_{33}\end{bmatrix}\]

우변을 곱한 결과는

\[\mathbf{A} = \begin{bmatrix}l_{11}^2 & l_{21}l_{11} & l_{31}l_{11} \\ l_{21}l_{11} & l_{21}^2 + l_{22}^2 & l_{31}l_{21} + l_{32}l_{22} \\l_{31}l_{11} & l_{31}l_{21} + l_{32}l_{22} & l_{31}^2 + l_{32}^2 + l_{33}^2\end{bmatrix}\]

그럼 다음과 같은 관계가 도출된다.

\[l_{11} = \sqrt{a_{11}},\;\; l_{22}=\sqrt{a_{22}-l_{21}^2}, \;\; l_{33}=\sqrt{a_{33} - (l_{31}^2) + l_{32}^2)}\]

이런 방식으로 어떠한 symmetric, positive definite \(3 \times 3\) 행렬에 대하여도 Cholesky 분해를 할 수 있다.

Cholesky 분해는 머신러닝에서 수 계산을 할 때 매우 중요한 도구이다! 예를 들어, 공분산 행렬은 symmetric positive definite 행렬인데, 많은 곱셈이 필요하다. 하지만 Cholesky 행렬을 통하면 가우시안 분산으로부터 샘플들을 생성할 수 있다든가(?), 랜덤 변수의 선형 변환을 가능하게 해서 오토인코더같은 통계 모델에서 그래디언트를 계산할 때 널리 사용된다든가 하는 것이다. (음..어렵네)

또, Cholesky 분해를 통해 determinant를 쉽게 계산할 수 있다. \(A=L L^{\top}\)일 때, \(\det{A} = \det({L})\det({L}^{\top})=\det(L)^2\)라는 걸 알고있다(이전 글에서 전치를 해도 determinant는 변하지 않는다고 배웠다). \(L\)은 triangular 행렬이기 때문에, determinant는 단지 대각요소들의 제곱의 곱인 \(\det(A)=\Pi_i l_{ii}^2\)가 된다! 대각행렬의 determinant는 대각 요소들의 곱이기 때문이다.

4.4 Eigendecomposition and Diagonalization

대각 행렬(diagonal matrix)은 대각 위치가 아닌 요소들이 모두 0인 행렬이다. 즉,

\[D=\begin{bmatrix} c_1 & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & c_n \end{bmatrix}\]

과 같은 형태이다. 대각 행렬의 determinant, powers, inverse는 빠르게 계산할 수 있다. determinant는 대각 요소들의 곱이며, 거듭제곱 \(D^k\)는 각 요소들의 \(k\) 제곱으로 표현되며, 대각 요소들이 모두 0이 아닐 경우 역함수 \(D^{-1}\)는 대각 요소들의 역수로 표현된다.

행렬을 어떻게 diagonal 형태로 변환할 수 있는지 살펴보자. \(A\), \(D\)가 similar 관계라고 하자.

Definition 2.22 (Similarity). 만약 \(\tilde{A}=S^{-1}AS\)인 regular(=invertible) 행렬 \(S \in \mathbb{R}^{n \times n}\)가 존재한다면, 두 행렬 \(A\), \(\tilde{A}\)은 similar하다.

Similarity에 대해서는 추후에 자세히 다뤄보도록 하고… 일단 \(D = P^{-1}AP\)를 만족하는 invertible 행렬 \(P\)가 있다고 하자. 좀 더 구체적으로는, \(A\)의 고유값들을 대각 요소로 갖는 대각 행렬 \(D\)이다. \(A\), \(D\)는 similar하다는 것을 잊지 말자.

Definition 4.19 (Diagonalizable). 만약 행렬 \(A \in \mathbb{R}^{n \times n}\)가 diagonal matrix와 similar이면, 즉, \(D = P^{-1}AP\)를 만족하는 invertible 행렬 \(P \in \mathbb{R}^{n \times n}\)이 존재하면 \(A\)는 diagonalizable하다.

이제부터 \(A \in \mathbb{R}^{n \times n}\)을 대각화(diagonalizing)하는 것이 다른 기저에서의 선형 매핑(Section 2.6.1)을 표현하는 방법이라는 것을 알아볼 것이다. 이는 \(A\)의 고유벡터로 구성된 기저가 된다는 사실!

\(A \in \mathbb{R}^{n \times n}\), \(\lambda_1, \cdots, \lambda_n\)라는 스칼라 집합, \(p_1, \cdots , p_n \in \mathbb{R}^{n}\)이라는 벡터 집합이 있다고 하자. \(P:=[p_1, \cdots, p_n]\), \(D \in \mathbb{R}^{n \times n}\)을 \(\lambda_1, \cdots, \lambda_n\)라는 대각 요소를 가진 대각 행렬이라고 정의하자. 만약 \(\lambda_1, \cdots, \lambda_n\)가 \(A\)의 고유벡터이고 \(p_1, \cdots, p_n\)가 이에 상응하는 \(A\)의 고유벡터라면, 다음을 보일 수 있다:

\[AP=PD\]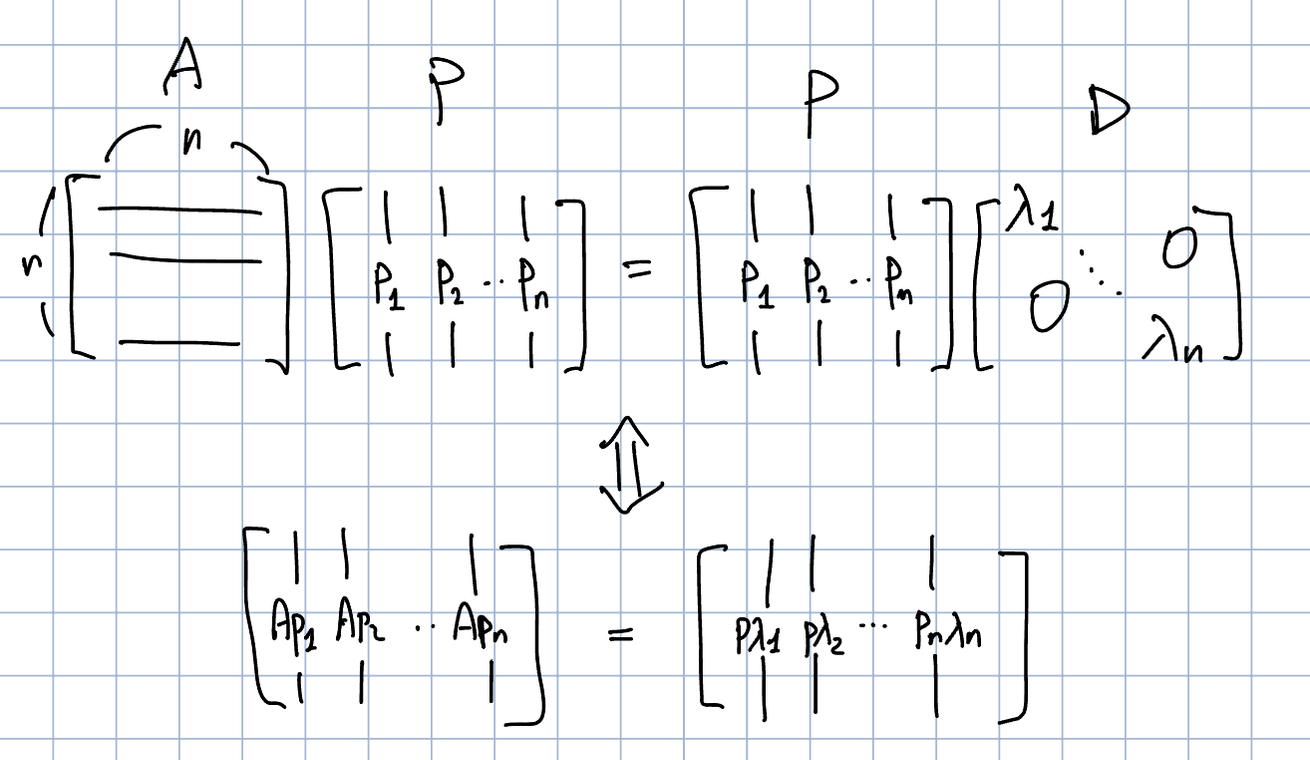

말은 복잡하지만, 결국 다음과 같이 표현만 바꾼 것이라고 보인다.

\[Ap_1 = \lambda_1 p_1 \\ Ap_2 = \lambda_2 p_2 \\ \vdots \\ Ap_n = \lambda_np_n\]

대각화(diagonalization) 정의는 \(P \in \mathbb{R}^{n \times n}\)가 invertible이어야만 한다.즉, \(P\)는 full rank(Theorem 4.3)여야 한다. \(n\)개의 선형 독립 고유벡터 \(p_1, \cdots, p_n\), 즉, \(p_i\)가 \(\mathbb{R}^{n}\)의 기저를 형성해야한다.

Theorem 4.20 (Eigendecomposition). 정방 행렬 \(A \in \mathbb{R}^{n\times n}\)은 다음과 같이 분해될 수 있다.

\[A = PDP^{-1}\]

\(P\in \mathbb{R}^{n \times n}\)이고 \(D\)는 대각 요소가 \(A\)의 고유값인 대각 행렬, \(A\)의 고유벡터가 \(\mathbb{R}^n\)의 기저를 형성해야 한다.

Theorem 4.20은 non-defective인 행렬만이 대각화 될 수 있고 \(P\)의 열벡터는 \(A\)의 \(n\)개의 고유벡터여야 한다는 것을 내포한다.

Symmetric 행렬에 대하여, 우리는 고유값 분해에 대해 심지어 더욱 강력한 결과를 얻을 수 있다.

Theorem 4.21. Symmetric 행렬 \(S \in \mathbb{R}^{n \times n}\)은 항상 대각화 될 수 있다.

위 정리는 spectral 정리 4.15로부터 곧바로 정리되는 것이다. 추가적으로, spectral 정리는 우리가 \(\mathbb{R}^n\)의 고유벡터의 ONB를 찾을 수 있다는 것을 의미한다. 즉, \(P\)는 orthogonal matrix(직교 행렬)가 되어, \(D=P^{\top}AP\)를 만족하게 된다.

Geometric Intuition for the Eigendecomposition

행렬의 eigendecomposition을 다음과 같이 해석할 수 있다: \(A\)가 표준 기저 관점에서의 선형 매핑의 변환 행렬이라고 하자. \(P^{-1}\)는 표준 기저로부터 eigenbasis로의 기저로의 기저 변환을 수행한다. 이는 고유벡터 \(p_i\) (빨간색, 오렌지색 화살표)를 표준 기저 벡터 \(e_i\)로 대응시킨다. 그 후, 대각행렬 \(D\)는 고유값 \(\lambda_i\)만큼 축방향으로 벡터의 크기를 변환시킨다. 마지막으로, \(P\)는 이렇게 크기가 바뀐 벡터들을 다시 표준 좌표계로 되돌리며 \(\lambda_iP_i\)로 만든다.

Example 4.11 (Eigendecomposition) \(A = \begin{bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix}\)의 eigendecomposition을 계산해보자. Step1 : 고유값과 고유벡터를 계산하자. \(A\)의 특성방정식은 다음과 같다.

\[\det(A - \lambda I) = \det \left( \begin{bmatrix} 2-\lambda & 1 \\ 1 & 2 - \lambda \end{bmatrix} \right) \\ =(2-\lambda)^2 - 1 \\ =\lambda^2 - 4\lambda + 3 \\ =(\lambda-3)(\lambda -1)\]

\(A\)의 고유값은 \(\lambda_1=1\)과 \(\lambda_2=3\)이 된다. 특성 방정식의 근이 곧 고유값이니 말이다. 그리고 고유벡터의 정의를 통해 다음을 계산하면,

\[\begin{bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix}p_1 = 1p_1,\;\;\;\begin{bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix}p_2=3p_2\]

를 계산한

\[p_1=\frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ -1 \end{bmatrix}, \;\;\; p_2=\frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ 1 \end{bmatrix}\]

가 고유벡터 \(p_1\), \(p_2\)를 계산할 수있다.

Step2 : 존재여부 판단. 고유벡터 \(p_1,\) \(p_2\)는 \(\mathbb{R}^2\)의 기저를 형성할 수 있다. 그러므로 \(A\)는 대각화 가능하다.

Step3 : \(A\)를 대각화하기 위해 행렬 \(P\)를 만든다. \(A\)의 고유벡터를 모아 \(P\)를 만들자.

\[P=[p_1, p_2] = \frac{1}{\sqrt{2}}\begin{bmatrix} 1 & 1 \\ -1 & 1 \end{bmatrix}\]

그러면 다음을 얻을 수 있다.

\[P^{-1}AP=\begin{bmatrix} 1 & 0 \\ 0 & 3 \end{bmatrix}=D\]

동일하게, 다음을 얻는다. (이 때는 \(P=P^{\top}\)이라는 것을 이용한다. 고유벡터 \(p_1\)과 \(p_2\)가 ONB를 구성하기 때문이다.)

\[\underbrace{\begin{bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix}}_{A} = \underbrace{\frac{1}{\sqrt{2}}\begin{bmatrix} 1 & 1 \\ -1 & 1 \end{bmatrix}}_{P} \underbrace{\begin{bmatrix} 1 & 0 \\ 0 & 3 \end{bmatrix}}_{D} \underbrace{\frac{1}{\sqrt{2}} \begin{bmatrix} 1 & 0 \\ 0 & 3 \end{bmatrix}}_{P^{\top}}\]

• 대각행렬 \(D\)의 제곱은 효율적으로 이루어진다. 그러므로, eigenvalue decomposition(만약 존재한다면)을 통해서 행렬 \(A \in \mathbb{R}^{n \times n}\)에 대한 행렬 제곱을 찾을 수 있다

  \[A^k=(PDP^{-1})^k=PD^kP^{-1}\]

  \(D^k\)를 계산하는 것은 효율적인데, 각각의 대각 요소에 제곱만 하면 되기 때문이다!

• eigendecomposition \(A=PDP^{-1}\)이 존재한다고 가정하자. 그럼,

  \[\det(A)=\det(PDP^{-1}) = \det(P)\det(D)\det(P^{-1})=\det(D)=\Pi_i d_{ii}\]

  위처럼 \(A\)의 determinant 계산이 쉬워진다.

고유값 분해는 정방행렬에 대해서만 사용된다. 일반적인 형태의 행렬을 분해하면 매우 유용할 것이다! 다음 챕터에서 일반적인 형태의 행렬 분해 방법인 singular value decomposition에 대해 알아본다!